How to make back-of-the-envelope calculations

The numbers to be found in the BioNumbers compendium and in the vignettes throughout this book can be thought of as more than simply data. They can serve as anchor points to deduce other quantities of interest and can usually be themselves scrutinized by putting them to a sanity test based on other numbers the reader may know and bring together by “pure thought”. We highly recommend the alert reader to try and do such cross tests and inferences. This is our trail-tested route to powerful numeracy. For example, in chapter 4 we present the maximal rates of chromosome replication. But one might make an elementary estimate of this rate by using our knowledge of the genome length for a bacterium and the length of the cell cycle. Of course, often such estimates will be crude (say to within a factor of 2), but they will be good enough to tell us the relevant order of magnitude as a sanity check for measured values.

There are many instances in which we may wish to make a first-cut estimate of some quantity of interest. In the middle of a lecture you might not have access to a database of numerical values, and even if you do, this skill of performing estimates and inferring the bounds from above and below as a way to determine unknown quantities is a powerful tool that can illuminate the significance of measured values.

One handy tool is how to go from upper and lower bound guesses to a concrete estimate. Let’s say we want to guess at some quantity.  Our first step is to find a lower bound.  If we can say that the quantity we are after is bigger than a lower bound x_L and smaller than an upper bound x_U, then a simple estimate for our quantity of interest is to take what is known as the geometric mean, namely,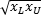

Though this may seem very abstract, in fact, in most cases we can ask ourselves a series of questions that allow us to guess reasonable upper and lower bounds to within a factor of 10. For example, if we wish to estimate the length of an airplane wing on a jumbo jet, we can begin with “is it bigger than 1 m?”.  Yes. “Is it bigger than 5 m?” Yes. “Is it bigger than 10 m?” I think so but am not sure. So we take 5 m as our lower bound. Now the other end, “is it smaller than 50 m?”  Yes.  “Is it smaller than 25 m?” I think so but am not sure. So we take 50 m as our upper bound. Using 5 m and 50 m as our lower and upper bounds, we then estimate the wing size as √5mx50m ≈ 15 m, the approximate square root of 250 m².  If we had been a bit more bold, we could have used 10 m as our lower bound with the result that our estimate for the length of the wing is ≈22 m. In both cases we are accurate to within a factor of 2 compared with the actual value, well within the target range of values we expect from “order-of-magnitude biology”.

Let’s try a harder problem, which will challenge the intuition of anyone we know. What would you estimate is the number of atoms in your body? 10¹⁰ is probably too low, sounds more like the number of people on earth. 10²⁰? Maybe, vaguely reminding us of the exponent in Avogadro’s number. 10⁸⁰ sounds way too high, such exponents are reserved for the number of atoms in the universe. 10⁴⁰? Maybe. So √ 10²⁰x10⁴⁰~10³⁰. A more solid calculation is given later in the book using the Avogadro constant (can you see how to do it?), but it suffices to say that we are within about two orders of magnitude of the correct order of magnitude and this based strictly on educated guessing. One may object to pulling 10²⁰ and 10⁴⁰ out of thin air. We claim this is exactly the kind of case where we have extremely little intuition and thus have nothing to start with aside from vague impression. But we can still construct bounds by eliminating estimates that are too small and too large as we did above, and somewhat surprisingly, with the aid of the geometric mean, that takes us close to the truth. One probably has to try this scheme out several times to check if the advertised effectiveness actually works. The geometric mean amounts really to taking the normal arithmetic mean in log space (i.e. on the exponents of 10). Had we chosen to take the normal mean on the values we guess themselves, our estimate would be completely dominated by the upper bound we choose, which often leads to extreme overestimation.

One of the questions that one might ask is how we know whether our estimates are actually “right”?  Indeed, often those who aren’t used to making estimates fear of getting the “wrong” answer. In his excellent book “Street Fighting Mathematics”, Sanjoy Mahajan makes the argument that an emphasis on this kind of “rigor” can lead in fact to mathematical “rigor mortis”. The strategy we recommend is to think of estimates as successive approximations, with each iteration incorporating more knowledge to refine what the estimate actually says.  There is no harm in making a first try and getting a “wrong” answer.  Indeed, part of the reason such estimates are worthwhile is that they begin to coach our intuition so that we can a priori have a sense of whether a given magnitude makes sense or not without even resorting to a formal calculation.