Rigorous Rules for Sloppy Calculations
One of the most important questions that every reader should ask themselves is: are any of the numbers in this book actually “right”? What does it even mean to assign numbers to quantities such as sizes, concentrations and rates that are so intrinsically diverse? Cellular processes show immense variability depending upon both the type of cell in question and the conditions to which it has been subjected. One of the insights of recent years that has been confirmed again and again is that even within a clonal population of cells there is wide cell-to-cell variability. Hence, both the diversity and intrinsic variability mean that the task of ascribing particular numbers to biological properties and processes is fraught with the danger of misinterpretation. One way to deal with this challenge is by presenting a range of values rather than “the value”. Not less important, a detailed discussion of the environmental conditions under which the cells grew and when and how the measurement was taken and analyzed is in order. Unfortunately, this makes the discussion very cumbersome and is often solved in textbooks and journals by avoiding concrete values altogether. We choose in this book to give concrete values that clearly do not give the “full” picture. We expect, and caution the reader to do the same, to think of them only as rough estimates and as an entry point to the literature. Whenever a reader needs to rely on a number for their research rather than merely get a general impression, he or she will need to turn to the original sources. For most values given in this book, finding a different source reporting a number that is a factor of two higher or lower is the rule rather than the exception. We find that a knowledge of the “order of magnitude” can be very useful and we give examples in the text. Yet, awareness of the inherent variability is critical so as not to get a wrong impression or perform inferences that are not merited by the current level of data. Variety (and by extension, variability) is said to be the spice of life – it is definitely evident at the level of the cell and should always be kept in the back of your mind when discussing values of biological properties.
How many digits should one include when reporting the measured value of biological entities such as the ones discussed throughout this book? Though this question might sound trivial, in fact there are many subtle issues we had to grapple with, that can affect the reader’s capability to use these numbers in a judicious fashion. To give a concrete example, say you measured the number of mitochondria in three cells and found 20, 26 and 34. The average is 26.666…, so how should you best report this result? More specifically, how many significant digits should you include to characterize these disparate numbers? Your spreadsheet software will probably entice you to write something like 26.667. Should it be trusted?
Before we dig deeper, we propose a useful conservative rule of thumb. If you forget everything we write below, try to remember this: it is usually a reasonable choice in reporting numbers in biology to use 2 significant digits. This will often report all valuable information without the artifact of too many digits giving a false sense of accuracy. If you write more than 3 we hope some inner voice will tell you to think hard what it means or just press the backspace key.
We now dive deeper. Significant digits are all digits that are not zero, plus zeros that are to the right of the first non-zero digit. For example, the number 0.00502 has three significant digits. Significant digits should supply information on the precision of a reported value. The last significant digit, that is the rightmost one, is the digit that we might be wrong about but it is still the best guess we have for the accurate value. To find what should be considered significant digits we will use a rule based on the precision (repeatability) of the estimate. The precision of a value is the repeatability of the measurement, given by the standard deviation or in the case of an average, by the standard error. If the above sentence confuses you, be assured that you are in good company. Keep on reading and make a mental note to visit Wikipedia at your leisure for these confusing terms as we do ourselves repeatedly.
Going back to the example above of counting mitochondria, a calculator will yield a standard deviation of 4.0552… The rule we follow is to report the uncertainty with one significant digit. Thus 4.0552 is rounded to 4 and we report our estimate of the average simply as 26, or more rigorously as 26±4. The last significant digit reported in the average (in this case 6) is at the same decimal position as the first significant digit of the standard error (in this case 4). We note that a leading 1 in some conventions does not count as a significant digit (e.g., writing 123 with one significant digit will be 120) and that in some cases it is useful to report the uncertainty with two digits rather than just one but that should not bother us further at this point. But be sure to stay away from using three or more digits in the uncertainty range. Anyone further interested can read a whole report (http://tinyurl.com/nwte4l5) from the Society of Metrology, the science of measurement.
Unfortunately, for many measured values relating to biology the imprecision is not reported. Precision refers to how much variation you have in your measurements whereas accuracy refers to how different it is from the real value. A systematic error will cause an inaccuracy but not an imprecision. Precision you can know from your measurements but for knowing accuracy you have to rely on some other method. You might want to add the distinction between accuracy and precision to your Wikipedia reading list, but bear with us for now. Not only is there no report of the imprecision (error) in most biological studies, but the value is often written with many digits, well beyond what should be expected to be significant given the biological repeatability of the experimental setting. For example, the average for the volume of a HeLa cell may be reported as 2854.3 µm3. We find, however, that reporting a volume in this way is actually misleading even if this is what the spreadsheet told the researcher. To our way of thinking, attributing such a high level of precision gives the reader a misrepresentation of what the measurement achieved or what value to carry in mind as a rule of thumb.
As the uncertainty in such measurements is often not reported we resort to general rules of thumb as shown in Figure 4. Based on reading many studies we expect many biological quantities to be known with only 2-fold accuracy, in very good cases maybe to 10% and in quite variable cases to within 5- or 10-fold accuracy. Low accuracy is usually not because of the tools of measurement that have very good precision but because systematic differences, say due to growth conditions being different, can lead to low accuracy with respect to any application where the value can be used. In this book we choose to make the effort to report values with a number of digits that implicitly conveys the uncertainty. The rules of thumb we follow are summarized in Figure 4 as a work flow to infer how many significant digits should be used in reporting a number based on knowing the uncertainty or guesstimating it. For example, say we expect the reported HeLa cell average volume to have 10% inaccuracy (pretty good accuracy for biological data), i.e., about 300 µm3. As discussed above we report the uncertainty using one significant digit, that is, all the other digits are rounded to zero. We can now infer that the volume should be written as 2900 µm3 (two significant digits). If we thought the value has a 2-fold uncertainty, i.e., about 3000 µm3, we will report the average as 3000 µm3 (one significant digit).
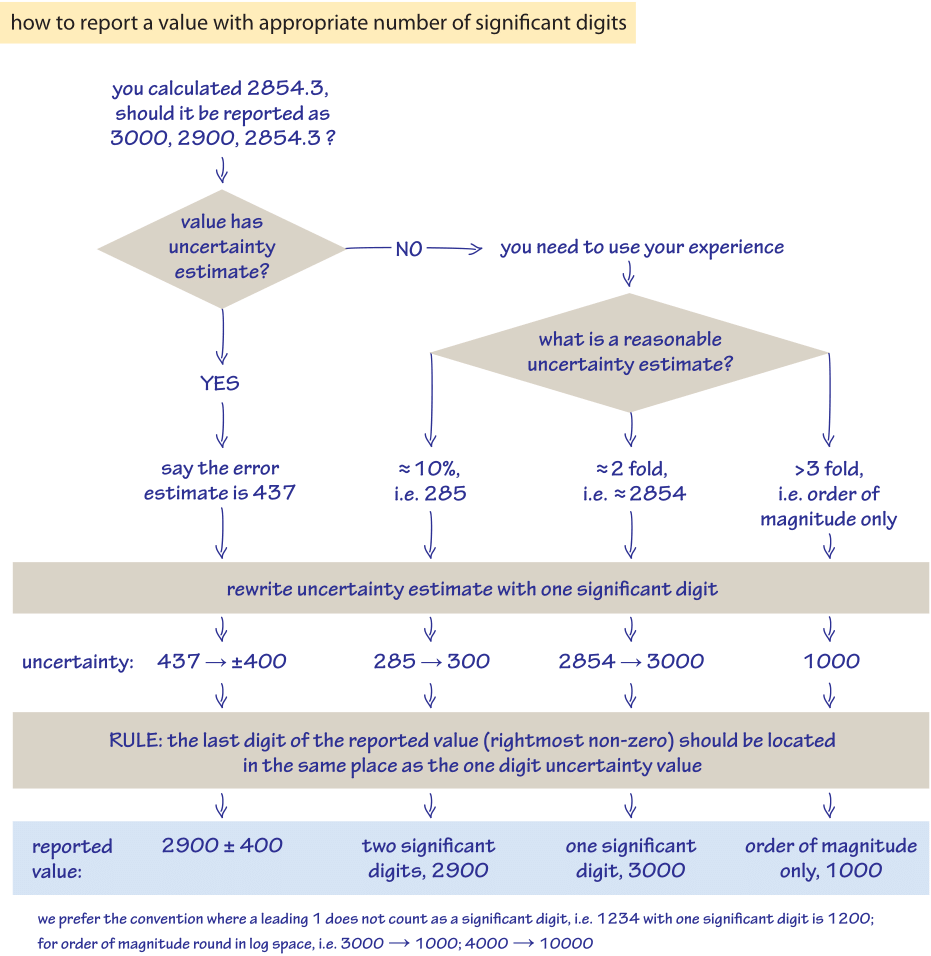
Figure 4: A flow chart to help determine how to report values with an appropriate number of significant digits
Finally, if we think there are very large imprecisions say to a factor of 5 or 10 we will resort to reporting only the order of magnitude, that is 1000 µm3, or better still to write it in a way that reflects the uncertainty as 103 µm3 We indicate only an order of magnitude in cases the expected imprecision is so large (practically, larger than 3 fold) that we cannot expect to have any sense of even one digit and have an estimate only of the number of digits in the accurate value. The digit 1 is special in the sense that it doesn’t mean necessarily a value of 1 but rather signifies the order of magnitude. So in such a case the number can be thought of as reported with less than one significant digit. Rounding can of course create a possible confusion. If you write 100, how do people know if this is merely an order of magnitude, or should be actually interpreted as precise to within 2 fold or maybe even 10% (i.e., also the following zero is precise)? In one convention this ambiguity can be solved by putting an underline for the last significant digit. So 100 shows the zero (and the 1) are significant digits, 100 shows the 1 is a significant digit whereas plain 100 is only to within an order of magnitude. We try to follow this convention in this book. Trailing zeros are by custom used as a replacement for the scientific notation (as in 3×103). The scientific notation is more precise in its usage of digits but less intuitive in many cases. The trailing zeros should not be interpreted as indicating a value of exactly zero for those digits, unless specifically noted (e.g., with an underline).
We often will not write the uncertainty, as in many cases it was not reported in the original paper the value came from, and thus we do not really know what it is. Yet, from the way we write the property value the reader can infer something about our ballpark estimate based on the norms above. Such an implicit indication of the expected precision should be familiar as in the example (borrowed from the excellent book “guesstimation”) of when a friend gives you driving directions and states you should be taking a left turn after 20 km. Probably when you reach 22 km and did not see a turn you would start to get worried. But if the direction was to take the turn after 20.1 km you would probably become suspicious before you reached even 21 km.
When aiming to find the order of magnitude we perform the rounding in log space, that is to say, 3000 would be rounded to 1000, while 4000 would be rounded to 10,000 (because log10(4)>0.5). We follow this procedure since our perception of the world as well as many error models of measurement methods are logarithmic (i.e., we perceive fold changes rather than absolute values). Thus the log scale is where the errors are expected to be normally distributed and the closest round number should be found. When performing a series of calculations (multiplying, subtracting, etc.) it is often prudent to keep more significant digits than in reporting final results and perform the rounding only at the end result stage. This is most relevant when subtraction cancels out the leading digits making the following digits critical. We are under the impression that following such guidelines can improve the quantitativehygiene essential for properly using and interpreting numbers in cell biology.

