How much force is applied by cytoskeletal filaments?
Force generation by cytoskeletal filaments is responsible for a diverse and important set of biological processes ranging from cell motility to chromosome segregation. These distinct mechanical functions are implemented by rich and complex structures (e.g. branched, crosslinked, etc.) in which the filaments are linked together in various arrangements. Whether we think of the forces exerted by actin filaments at the leading edge of motile cells or the complicated arrangement of forces applied by microtubules during the process of chromosome segregation, understanding the basis and limits of force generation is a central pillar of modern cell biology.
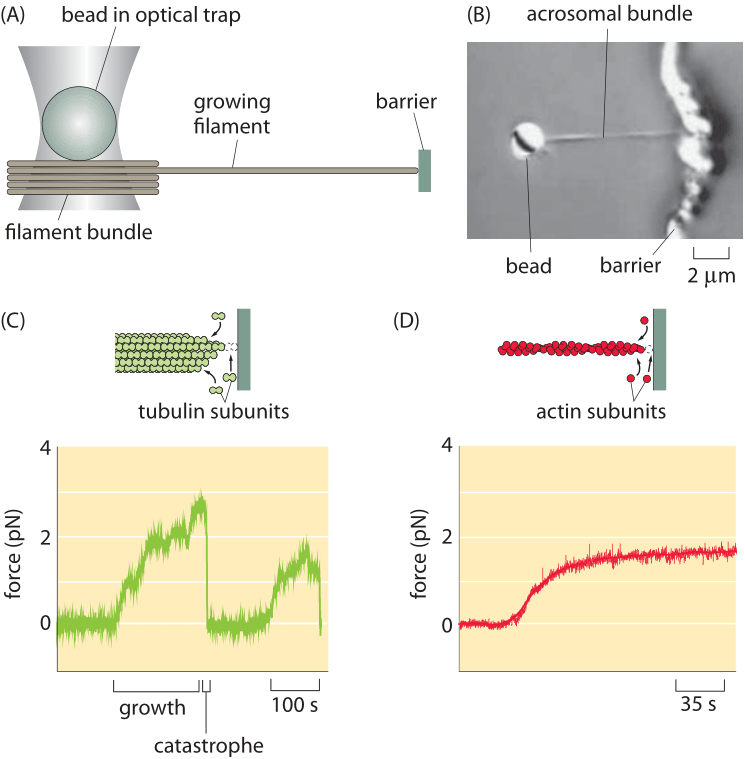
Figure 1: Optical-trap measurement of the force of polymerization. (A) Schematic of the use of an optical trap to measure forces as the filament grows into an obstacle. (B) Microscopy image of a bead (2 μm diameter) with attached acrosomal bundle. (c) Time evolution of the force during growth and catastrophe of microtubules. (D) Force build up over time for actin polymerization. (Adapted from (A), (C) J. W. Kerssemakers et al., Nature 442:709, 2006; (B) and (D) M. J. Footer et al., Proc. Nat. Acad. Sci. 104:2181, 2007.)
Recent years have seen a steady stream of clever ideas for measuring how force is generated by the filaments of the cytoskeleton. Specifically, a series of beautiful measurements have made it possible to query the forces applied by bundles of cytoskeletal filaments and more amazingly, of individual filaments, engaged in the process of polymerization. Like with many force measurements, conceptually the idea is to use the deflection of a calibrated spring to read out the forces. Measurements on cytoskeletal filaments have exploited such generalized springs in several different ways. First, in optical traps, laser light can be used to trap a micron-sized bead, which can then be used as a “spring” to read out the forces of growing cytoskeletal filaments as they push against it. For small displacements of the bead away from the laser focus, there is a linear restoring force tending to push the bead back to the focus. As a result, bead displacement can serve as a surrogate for force itself. Using a setup like that shown in Figure 1A, the force generation due to individual filaments has been measured directly by permitting the cytoskeletal filament to crash into a barrier during the process of polymerization. As the elongation proceeds the restoring force exerted by the bead increases until it reaches the maximal force that can be overcome by the polymerization of the filament – the so-called stall force. At this point the collision dynamics resets as shown in Figure 1B in what is known as a shrinkage catastrophe. Such measurements result in a characteristic force scale of order 5 pN, comparable to the forces exerted by the more familiar translational motors such as myosin and kinesin. This value can be compared to the energy driving filament construction usually based on ATP or GTP hydrolysis. Such hydrolysis reactions provide roughly 20 kBT of free energy per nucleotide hydrolyzed and should be compared to the work done by a force of 5pN acting over a monomer extension length which is about 4 nm, i.e. 20 pN x nm. In our tricks of the trade introduction we refer to the rule of thumb that kBT is roughly equal to 4 pN nm and thus the filament force acting over the 4 nm distance corresponds to a free energy of about 5 kBT. Given that the energy conversion is not perfect this seems like a very reasonable correspondence between the free energy available from nucleotide hydrolysis and the work done by the polymerizing filament.
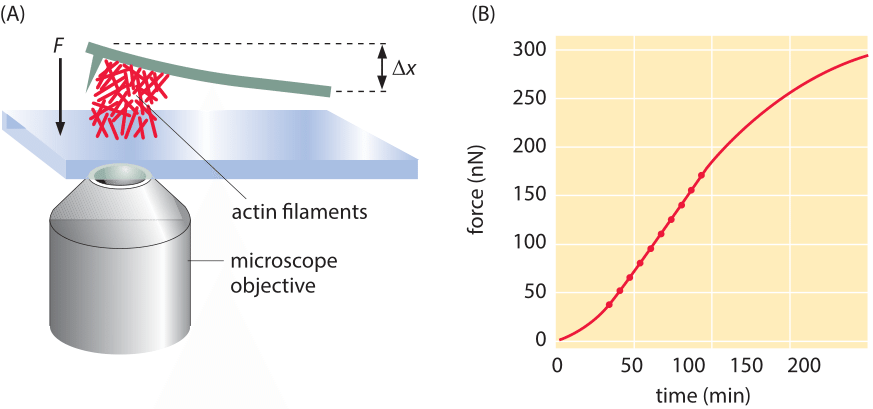
Figure 2: Force due to polymerization of a bundle of actin filaments. (A) Schematic of the geometry of force measurement using a calibrated cantilever. (B) Measurement of the build up of force over time. Note that the number of filaments schematically drawn in (A) is orders of magnitude lower than the actual number that created the actual force measured in B. (Adapted from S. H. Parekh et al., Nat. Cell Biol. 7:1219, 2005).
Often, the behavior of cytoskeletal filaments is dictated by their collective action rather than by the properties of individual filaments. A veritable army of different proteins can alter the arrangements of cytoskeletal filaments by capping them, crosslinking them, nucleating branches and a host of other alterations, thus shaping their force-generating properties. To measure the collective effects that emerge when more than one cytoskeletal filament is acting in concert, another clever “spring” was devised. This time the spring results from the deflection of a small (approximately 20 micron) cantilever when pushed on by an array of filaments as indicated schematically in Figure 2. The concept is that a collection of actin filaments is seeded on the surface beneath the cantilever and then as the filaments polymerize, they make contact with the cantilever and bend it upwards. As can be seen in the figure, when many such filaments work together, the resulting force scale is tens of nN rather than several pN as was found in the case of individual filaments.
What can a handful of pN buy you? A characteristic mammalian cell has a mass of a few ng (i.e. few 10-12 kg), corresponding to a weight of W=m x g=10-12 kg x 10 m/s2 = 10 pN. We can fancifully state that a few filaments can already hold a cell against gravity’s pull just like professional rock climbers can stabilize themselves over a cliff with one hand. Beyond the cellular drama, this simple estimate helps us realize why the force of gravity is usually not of much consequence in the lives of cells. The prevailing forces on components in the cellular environment are much higher than those produced by gravity.

