Size and Geometry Introduction

In this chapter, all of our vignettes center in one way or another on the simple question of “how big”. J. B. S Haldane, when he wasn’t busy with inventing population genetics or formulating the theory of enzyme kinetics (among many other things), wrote a delightful essay entitled “On being the right size”. There, he discusses how size is critical in understanding functional constraints on animals. For example, Haldane notes that when a human steps out of water, because of surface tension he or she carries roughly a pound of water with them.  On the other hand, an insect would carry comparatively much more, covered by about its own weight in water.  The functional implications are often dire. In this same spirit, we aim to characterize the sizes of things in molecular and cellular biology with the hope of garnering insights into the kinds of functional implications explained by Haldane at larger scales.

Biological structures run the gamut in sizes from the nanometer scale of the individual macromolecules of life all the way up to the gigantic cyanobacterial blooms in the ocean that can be seen from satellites.  As such, biologists can interest themselves in phenomena spanning more than 15 orders of magnitude in length scale. Though we find all of these scales fascinating (and important), in this book we primarily focus on those length scales that are smaller than individual organisms as depicted in Figure 1.

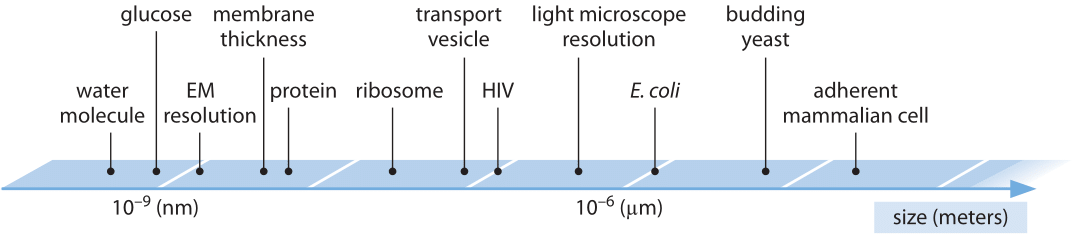
Figure 1: Range of characteristic sizes of the main biological entities relevant to cells. On a logarithmic scale we depict the range from single molecules serving as the nuts and bolts of biochemistry, through molecular machines, to the ensembles which are cells.

One dilemma faced when trying to characterize biological systems is the extent to which we should focus on model systems.  Often, the attempt to be comprehensive can lead to an inability to say anything concrete. As a result, we aim to give an intimate quantitative description of some common model cells and organisms, punctuated here and there by an attempt to remind the reader of the much larger diversity that lies beyond. We suggest that in those cases where we don’t know better, it is very convenient to assume that all bacteria are similar to E. coli.  We make this simplification for the sake of providing a general order-of-magnitude idea of the numbers that characterize most bacteria. In the same vein, our picture of a mammalian cell is built around the intuition that comes from using HeLa cells as a model system. One can always refine this crude picture when more information becomes available on say the volume or geometry of a specific cell line of interest. The key point is to have an order of magnitude to start with. A similar issue arises when we think about the changes in the properties of cells when they are subjected to different external conditions. Here again we often focus on the simplified picture of happily dividing, exponentially growing cells, while recognizing that other conditions can change our picture of the “average” cell considerably. The final issue along this progression of challenges having to do with how to handle the diversity of biological systems is how we should deal with cell-to-cell variation – how much do individual cells that have the same genetic composition and face the same external conditions vary? This chapter addresses these issues through a quantitative treatment both for cell size and protein abundance.

The geometries of cells come in a dazzling variety of different shapes and sizes.  Even the seemingly homogeneous world of prokaryotes is represented by a surprising variety of shapes and sizes. But this diversity of size and shape is not restricted only to cells. Within eukaryotic cells are found organelles with a similar diversity of form and a range of different sizes. In some cases such as the mitochondria, chloroplasts (and perhaps the nucleus), the sizes of these organelles are similar to bacteria, which are also their evolutionary ancestors through major endosymbiotic events.  At smaller scales still, the macromolecules of the cell come into relief and yet again, it is found that there are all sorts of different shapes and sizes with examples ranging from small peptides such as toxins to the machines of the central dogma to the assemblies of proteins that make up the icosahedral capsids of viruses.

In thinking of geometrical structures, one of the tenets of many branches of science is the structure-function paradigm, the simple idea that form follows function. In biology, this idea has been a part of a long “structural” tradition that includes the development of microscopy and the emergence of structural biology. We are often tempted to figure out the relative scales of the various participants in some process of interest. In many of the vignettes we attempt to draw a linkage between the size and the biological function.

Interestingly, even from the relatively simple knowledge of the sizes of biological structures, one can make subtle functional deductions. For example, what governs the burst size of viruses (i.e. the number of viruses that are produced when an infected cell releases newly synthesized viruses)? Some viruses infect bacteria whereas others infect mammalian cells, but the sizes of both groups of viruses are relatively similar, whereas the hosts differ in size by a characteristic volume ratio of 1000. This helps explain the fact that burst sizes from bacteria are about 100 whereas in the case of mammalian cells the characteristic burst size is ≈100,000.  Throughout the chapter, we return to this basic theme of reflecting on the biological significance of the many length scales we consider.

In moving from the intuitive macroscopic world into the microscopic domain a critical intellectual linkage will often be provided by Avogadro’s number (see the preface for historical efforts to determine its value). This important constant is defined as the number of hydrogen atoms with a mass of one gram. With a value of about 6×10²³, this conversion factor reveals itself time and again and the conversion was shown in the opening chapter.