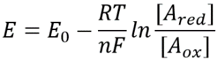What is the redox potential of a cell?

Redox potentials are used to characterize the free energy cost and direction of reactions involving electron transfer, one of the most ubiquitous and important of biochemical reactions. Such reduction-oxidation reactions are characterized by a free energy change that shares some conceptual features with that used to describe pKa in acid-base reactions where proton transfer is involved rather than electron transfer. In this vignette, one of the most abstract in the book, we discuss how the redox potential can be used as a measure of the driving force for a given oxidation-reduction reaction of interest.  By way of contrast, unlike the pH, there is no sense in which one can assign a single redox potential to an entire cell.

The redox potential, or more accurately the reduction potential, of a compound refers to its tendency to acquire electrons and thereby to be reduced. Some readers might remember the mnemonic “OILRIG” which reminds us that “oxidation is loss, reduction is gain”, where the loss and gain are of electrons. Consider a reaction that involves an electron transfer: A_ox + ne^– ↔ A_red where n electrons are taken up by the oxidized form (A_ox) to give the reduced form (A_red) of compound A. The redox potential difference ΔE between the electron donor and acceptor is related to the associated free energy change ΔG of the reaction via ΔG=nFΔE where n is the number of electrons transferred and F is Faraday’s constant (96,485 J/mol/V or ≈100 kJ/mol/V). By inspecting tabulated values of these potentials, it is possible to develop an intuition for the tendency for electron transfer and hence, of the direction of the reaction.

Figure 1: A “redox tower” showing the redox potential of common metabolic half reactions. Metabolic processes can be seen as moving electrons between molecules, often capturing some of the energy released as the electrons move from high energy to lower energy states as in glycolysis or respiration. Electrons donated by the “half-reactions” on top can be consumed in a half-reaction lower on the tower to complete a thermodynamically favorable reaction. For example, the net process of glycolysis involves the oxidation of glucose to pyruvate coupled to the reduction of NAD+ to NADH. Since the oxidation of glucose lies at the top of the tower and the reduction of NAD+ is below it, this electron flow is thermodynamically favorable. Comparing to the ATP hydrolysis scale bar we can also see that this electron flow is favorable enough to generate ATP. Aerobic respiration involves many intermediate electron transfers through the electron transport chain. Several of these transitions are shown, including the oxidation succinate to fumarate which is mechanistically coupled to the reduction of ubiquinone to ubiquinol in the inner mitochrondrial membranes. Each of these intermediate electron transfers must be thermodynamically favorable on its own in order for respiration to proceed. By comparing to the “ATP hydrolysis scale” we can see that the individual transformations in the electron transport chain are not energetic enough to generate ATP on their own. Yet they are favorable enough to pump a proton across the cell or mitochondrial membrane. This is the energetic basis for chemiosmosis: cells store quanta of energy too small for ATP synthesis in the proton gradient across a membrane. That energy is later used to generate ATP by converting the H+ gradient into phosphoanhydride bonds on ATP through the ATP synthase.

Though ATP is often claimed to be the energy currency of the cell, in fact,  for the energetic balance of the cell the carriers of reducing power are themselves no less important. The most important example of these carriers is the molecule NADH in its reduced or oxidized (NAD⁺) forms. We can use the redox potential to connect these two molecular protagonists, and estimate an upper bound on the number of ATP molecules that can be produced from the oxidation of NADH (produced, for example, in the TCA cycle). The NAD⁺/NADH pair has a redox potential of E = -0.32 V and it is oxidized by oxygen to give water (protons coming from the media) with a redox potential of E = +0.82 V. Both are shown in Figure 1 as part of a “redox tower” of key biological half reactions that can be linked to find the overall redox potential change and thus the free energy. For the reaction considered above of NADH oxidation by oxygen, the maximal associated free energy that can be extracted is thus

ΔG = n x F x ΔE = 2 x 100 kJ/(molxV) x (0.82-(-0.32)) V = 230 kJ/mol≈ 90 k_BT,

where n=2 and F≈100kJ/mol/V. As ATP hydrolysis has a free energy change of ≈50kJ/mol under physiological conditions we find that 228 kJ/mol suffices to produce a maximum of 228/50≈4.5 ATPs. In the cell, oxidation of NADH proceeds through several steps in respiration and results in the transfer of 10 protons across the membrane against the electro-chemical potential (BNID 101773). These proton transfers correspond to yet another way of capturing biochemical energy. This energy is then used by the ATPase to produce 2-3 ATPs. We thus find that about half of the energy that was released in the transfer of electrons from NADH to oxygen is conserved in ATP. Ensuring that the reaction proceeds in a directional manner to produce ATP rather than consume it requires that some of the energy is “wasted” as the system must be out of equilibrium.

Why should one discuss redox potentials of half reactions and not free energies of full reactions? The units themselves owe their origins to the ability in the field of electrochemistry to measure in the lab the voltage difference, i.e. the potential measured in volts, across two chambers that contain different electron carriers, and to stop the net reaction with a voltage. The usefulness of redox potentials for half reactions lies in the ability to assemble combinations of different donors and acceptors to assess the thermodynamic feasibility and energy gain of every considered reaction. If you have k possible electron transfer compounds, the ~k² possible reactions can be predicted based on only the k redox potentials.

Just as we speak of the pH of a solution, at first guess, we might imagine that it would be possible to speak of an apparently analogous redox potential of the cell. Knowing the concentration of the reduced and oxidized forms of a given reaction pair defines their pool redox potential via the relation

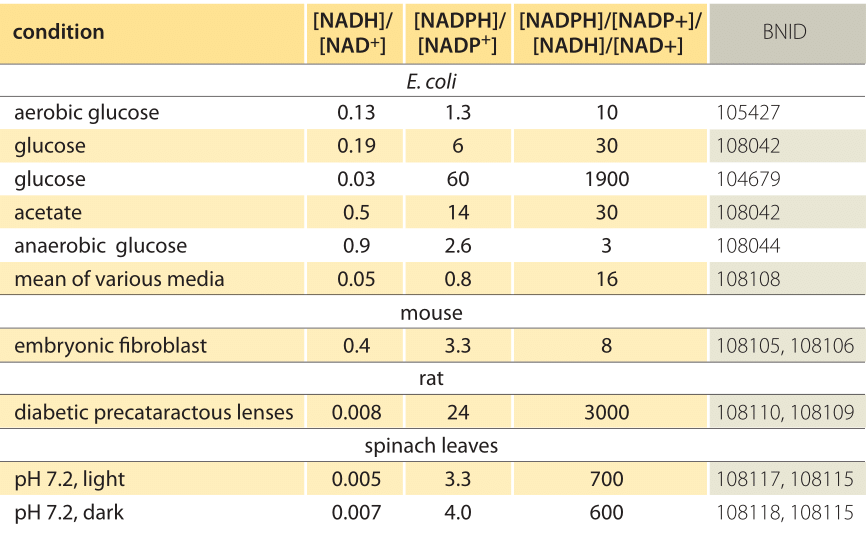
Table 1: concentration ratios of the common electron donor pairs NAD/NADH and NADP/NADPH. As can be seen the first is relatively oxidized and the second relatively reduced with a ratio among them usually much larger than 1.

This equation (a so-called Nernst equation) provides the value of the redox potential under concentration conditions typical of the cell as opposed to the standard state conditions (where by definition [A_red]=[A_ox]). As an example, consider the donation of an electron to NAD⁺ resulting in the oxidized form NADH. In the mitochondrial matrix a ratio of 10-fold more of the oxidized form is reported (BNID 100779) as shown in Table 1. In this case, we find the factor  is ≈30 mV and thus the redox potential changes from -0.32 V to -0.29 V. To make sure the direction of effect we got is sensible we notice that with an overabundance of the oxidized form the tendency to be oxidized by oxygen is somewhat lower as seen by the fact that the redox potential is now closer than before to that of the oxygen/water electron exchanging pair (+0.82V).

A cell is not at equilibrium and there is weak coupling between different redox pairs. This situation leads to the establishment of different redox potentials for coexisting redox pairs in the cell. If the fluxes of production and utilization of the reduced and oxidized forms of a redox pair, A_red and A_ox and another B_red and B_ox, are much larger than their interconversion flux, A_red+B_ox<–>A_ox+B_red then A and B can have very different redox potentials. As a result it is ill defined to ask about the overall redox potential of the cell as it will be different for different components within the cell. By way of contrast, the pH of the cell (or of some compartment in it) is much better defined since water serves as the universal medium that couples the different acid-base reactions and equilibrates what is known as the chemical potential of all species.

For a given redox pair in a given cell compartment the concentration ratio of the two forms prescribes the redox potential in a well-defined manner. Compounds that exchange electrons quickly will be in relative equilibrium and thus share a similar redox potential. To see how these ideas play out, it is thus most useful to consider a redox pair that partakes in many key cellular reactions and, as a result, is tightly related to the redox state of many compounds. Glutathione in the cytoplasm is such a compound as it takes part in the reduction and oxidation of the highly prevalent thiol bonds (those containing sulfur) in cysteine amino acids of many proteins. Glutathione is a tripeptide (composed of 3 amino acids), the central one a cysteine which can be in a reduced (GSH) or oxidized form where it forms a dimer with a cysteine from another glutathione molecule (denoted GSSG). The half reaction for glutathione is thus 2 x GSH <-> GSSG + 2e^– + 2H⁺. The other half reaction is often a sulfur bond that is “opened up” in a receptive protein thus being kept in the reduced form owing to the constant action of glutathione. Glutathione is also a dominant player in neutralizing reactive compounds that have a high tendency to snatch electrons and thus oxidize other molecules. Such compounds are made under oxidative stress as for example when the capacity of the electron transfer reactions of respiration or photosynthesis is reached. Collectively called ROS (reactive oxygen species) they can create havoc in the cell and are implicated in many processes of aging. The dual role of glutathione in keeping proteins folded properly and limiting ROS as well as its relatively high concentration and electron transfer reactivity make it the prime proxy for the redox state of the cell. The concentration of glutathione in the cell is ≈10mM (BNID 104679, 104704, 111464), making it the second most abundant metabolite in the cell (after glutamate) ensuring that it plays a dominant role as an electron donor in redox control of protein function. In other functions of cells there are other dominant electron pairs. In biosynthetic anabolic reactions the NADP⁺/NADPH pair and in breakdown catabolic reactions it is NAD+/NADH.

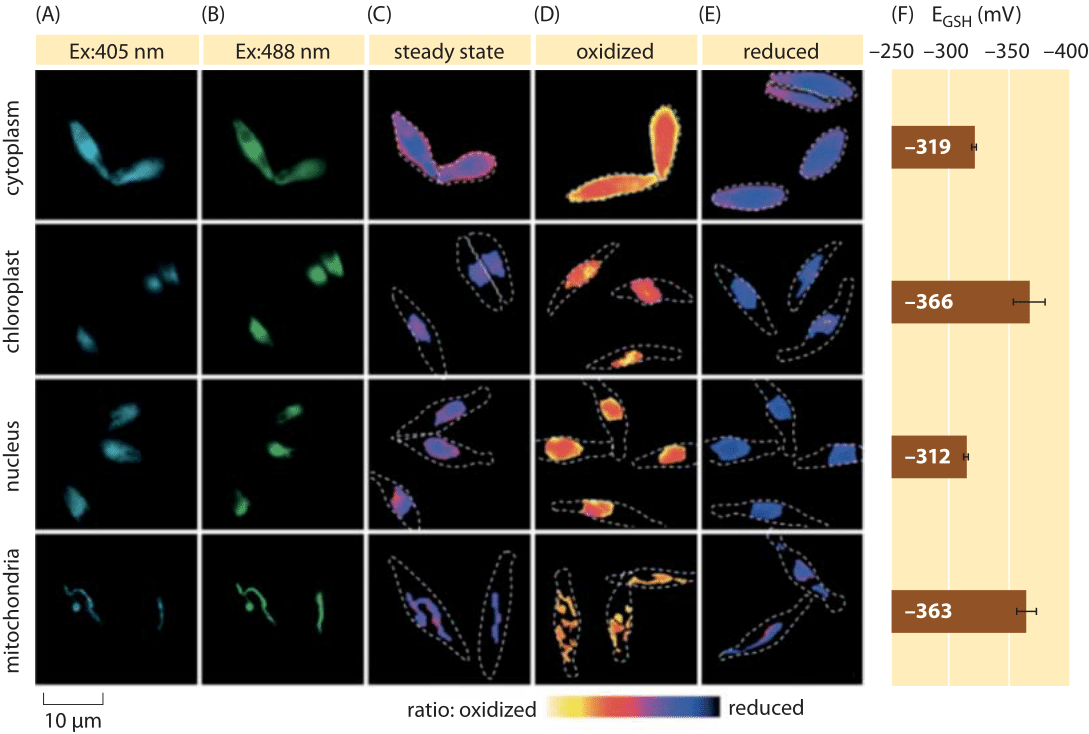
Figure 2: Imaging of subcellular redox potential of the glutathione pool in diatom algae in vivo. Fluorescence microscopy imaging of P. tricornutum cells expressing roGFP2 in various subcellular localizations. Fluorescence images at two excitation wavelengths (A, B), were divided to obtain ratiometric values (C). For calibration, ratiometric images are captured under strong oxidant (150 mM H2O2) (D) and reductant (1 mM DTT) (E) conditions. Dashed lines represent the cells’ outline, drawn based on the bright field images. (F) Steady-state redox potential of the glutathione pool, EGSH in mV, was calculated based on the Nernst equation using the oxidation level under given pH values for each organelle. Adapted from: S. Graff van Creveld et al., ISME J., 9:385, 2015.

How does one go about measuring redox potentials in living cells? Yet another beneficiary of the fluorescent protein revolution was the subject of redox potentials. A reporter GFP was engineered to be redox sensitive by incorporation of cysteine amino acids that affect the fluorescence based on their reduction by the glutathione pool. Figure 2 shows the result of using such a reporter to look at the glutathione redox potential in different compartments of a diatom.

From measurements of the redox state of the glutathione pool in different cellular organelles and under varying conditions we can infer the ratio of concentrations of the reduced to oxidized forms. Values range from about -170 mV in the ER and in apoptotic cells to about -300 mV in most other organelles and in proliferation cells (BNID 103543, 101823, 111456, 111465). Given that the standard redox potential of glutathione is -240 mV (BNID 111453, 111463), what then is the ratio of reduced to oxidized glutathione? Using the Nernst equation (or equivalently, from the Boltzmann distribution), a ten-fold change in the product/reactant ratio corresponds to an increase of ≈6 kJ/mol in free energy (≈2 k_BT). Given the 2 electrons transferred in the GSH/GSSG reaction this concentration ratio change is usually equal to 30mV, though for glutathione, the stoichiometry of 2 GSH molecules merging to one GSSG covalently-bound molecule makes this only an approximation. The 100 mV change reported across conditions reflects a ratio of concentrations between about equal amounts of the reduced and oxidized forms (in apoptotic cells) to over 1,000 fold more concentration of the reduced form. Indeed in most cellular conditions the oxidized form is only a very small fraction of the overall pool but still with physiological implications.

One confusing aspect of redox reactions is that the transfer can take several forms. In one case it is only electrons as in the reactions carried out by cytochromes in electron transfer chains. In another common case it is a combination of electrons and protons as in the cofactor NAD⁺/NADH where two electrons and one proton (H⁺) are transferred. Finally, there are the reactions where the same number of electrons and protons is transferred when one would naturally be tempted to discuss transfer of hydrogens. This is for example the case for the overall reaction of glucose oxidation where oxygen is reduced to water. Two hydrogens have thus been transferred, so should one discuss the transfer of electrons, hydrogens or protons? The definition of the redox potential (given above) focuses only on the electron “state”. What about the protons and what happens to these when one encounters a chain of electron transfer reactions where some intermediate compounds contain the hydrogen protons and some do not? The explanation resides in the surrounding water and their pH. The reaction occurs at a given pH, and the reacting compounds are in equilibrium with this pH and thus giving off or receiving a proton has no effect on the energetics. The aqueous medium serves as a pool where protons can be “parked” when the transfer reaction is solely of electrons (the analogy borrowed from the very accessible introductory biochemistry book “The chemistry of life” by Steven Rose). These parked protons can be borrowed back at subsequent stages as occurs in the final stage of oxidative respiration where cytochrome oxidase takes protons from the medium. Because one assumes that water is ubiquitous one does not need to account for protons except for knowing the prevailing pH which depicts the tendency to give or receive protons. This is the reason why we discuss electron donors and acceptors rather than hydrogen donors and acceptors.