What is the energy of a hydrogen bond?
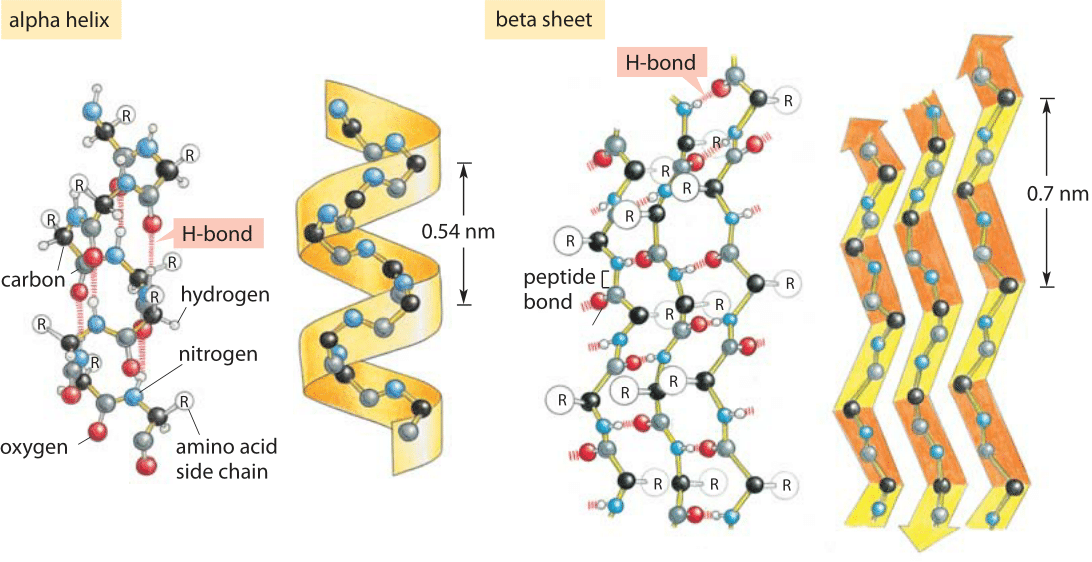
Figure 1: Hydrogen bonding and protein secondary structure. Alpha helix and beta sheet structures both depend upon hydrogen bonding as labeled in both schematics. (Adapted from MBOC)
Hydrogen bonds are ubiquitous and at the heart of many biological phenomena such as the formation of the alpha-helix and beta-sheet secondary structures in proteins as shown in Figure 1. Similarly, the binding of base pairs in DNA that holds the double helix together is based on every adenine forming two hydrogen bonds with thymidine and every cytosine forming three hydrogen bonds with guanine as depicted in Figure 2. The binding of transcription factors to DNA is often based on formation of hydrogen bonds reflecting a nucleic acid-protein form of hydrogen bonding. These bonds govern the off-rate for transcription factor unbinding and thus the dissociation constant (with the on-rate often being diffusion limited and thus nonspecific to the binding site). In addition, hydrogen bonds are often central to the function of catalytic active sites in enzymes.
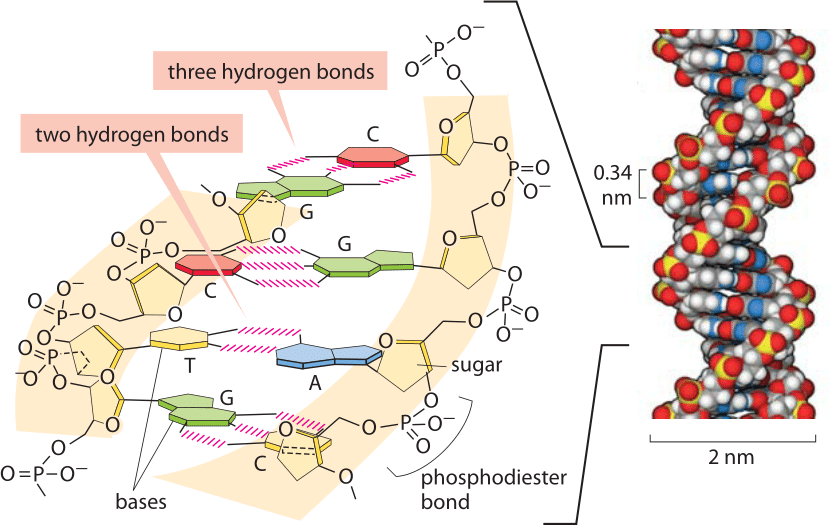
Figure 2: Base pairing in the double helix. Illustration of how bases are assembled to form DNA, a double helix with two “backbones” made of the deoxyribose and phosphate groups. The four bases form stable hydrogen bonds with one partner such that A pairs only with T and G pairs with C. A space-filling atomic model approximating the structure of DNA is shown on the right. The spacing between neighboring base pairs is roughly 0.34 nm. (Adapted from PBOC)
Because of the high frequency of hydrogen bonding in the energy economy of cells, it is natural to ask how much free energy is associated with the formation of these bonds. Indeed, the energy scale of these bonds, slightly larger than the scale of thermal energies, are central to permitting the transient associations so typical of macromolecular interactions and that would be completely forbidden if these bonds were based upon covalent interactions instead. Though the length of hydrogen bonds is quite constant at ≈0.3 nm (BNID 108091), their energies defy simple and definitive characterization. This provides a challenging and interesting twist on this most basic of biological interactions. One of the ways to come to terms with the nuance in the free energy of hydrogen bonding is to appreciate that the members of a hydrogen bond can interact with their environment in many different ways. If a hydrogen bond is broken, the two members will form alternative hydrogen bonds with the surrounding solvent – water. But this raises the following question: if the dissolution of a hydrogen bond results in the formation of other hydrogen bonds what is the source of any associated free energy change? In fact, such bonding rearrangements alter the level of order in the solvent and thus the entropy can be the dominant free energy contribution.
Given the strong context dependence of the strength of hydrogen bonding, this becomes one of those cases in our book where order-of-magnitude thinking is more useful and honest than the attempt to provide one definitive number. A rule of thumb range for the energies associated with hydrogen bonds is 6-30 kJ/mol (≈2-12 kBT) (BNID 105374, 103914, 103913).
To get a better sense of the magnitude of hydrogen bond energies, we consider biology’s iconic great molecule of DNA. From the moment of its inception, the structure of DNA implied stories about how the molecule works. That is, through stacks of base pairs, the double helix hides within itself a model of how it might be replicated. As noted above, AT pairing is characterized by two hydrogen bonds whereas CG base pairing is characterized by three such bonds as shown in Figure 2. One of the first things that any student learns when joining a molecular biology lab is how to use a PCR machine and one of the first bits of training that goes with it is programming that machine to go through its rhythmic changes in temperature as the double-helix is melted and annealed again and again. What sets the temperatures used? In a word, the AT content of the sequence of interest, reflecting in turn both the number of hydrogen bonds that have to be disrupted and the strength of base stacking, another important biophysical process governing DNA stability (BNID 111667).
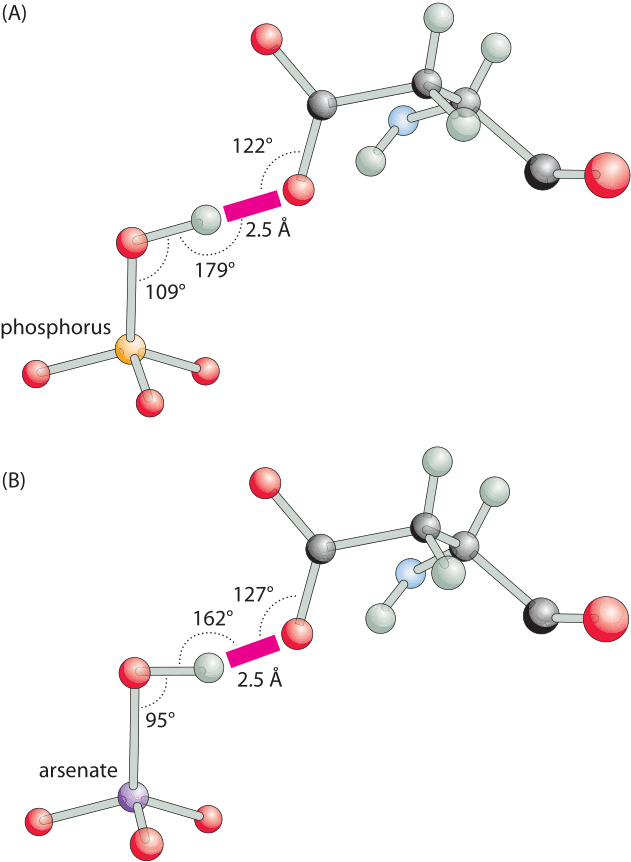
Figure 3: Hydrogen bonding angles for a phosphate binding protein are close to optimal in the phosphate-bound structure but distorted with arsenate. (A), A close-up view of the short hydrogen bond between oxygen of a bound phosphate and the carboxylate of aspartate. The binding angles are close to the canonical optimal values. (B), The same bond in the arsenate-bound structure, has a distorted suboptimal interaction angle. This difference can readily account for the ≈500 fold difference in favor of phosphate binding over arsenate. (Adapted from: M. Elias et al., Nature 491:134, 2012.)
An even more compelling example of the magnitude of the base pairing effect is to use it to think about the specificity of codon-anticodon recognition in translation. The triplet pairing rule for tRNAs to recognize their mRNA partners are based upon each of the three bases pairing with its appropriate partner. But let’s see how much discriminatory power such bonding is worth. For example, what happens when a CG base pair is replaced by an incorrect CT “base pair”? Now, many things change, but at least one hydrogen bond that should be present is no longer there. The Boltzmann distribution tells us how to evaluate the relative probability of different events as p(1)/p(2)=exp(-ΔE/kBT), where ΔE is the energy difference between those two states. If ΔE≈-6 kJ/mol (=-2.3 kBT), a lower end value for hydrogen bond energies, this implies a 10-fold difference in the two probabilities resulting is much higher and requires the energy driven mechanism of kinetic proofreading. The beauty of this simple estimate is that it shows how the machinery of the Boltzmann distribution can be used to connect changes in hydrogen bonding energies to different levels of molecular discrimination.
The importance of hydrogen bonds lies not only in their energy, which leads to favorable binding, but also in their strong dependence on conformation. A slight change in the angle or distance between the relevant atoms and the energy will change drastically. For example, as shown in Figure 3, a hydrogen bond is the key element for specificity in a transporter protein that has to differentiate between two chemical groups of very similar size and charge, namely, phosphate and arsenate. A change in angle and distance can result in orders of magnitude differences in the binding strength, making these bonds a key element conferring specificity. The spatial dependence is much weaker for other free energy contributions such as the hydrophobic effect discussed in the next vignette.

