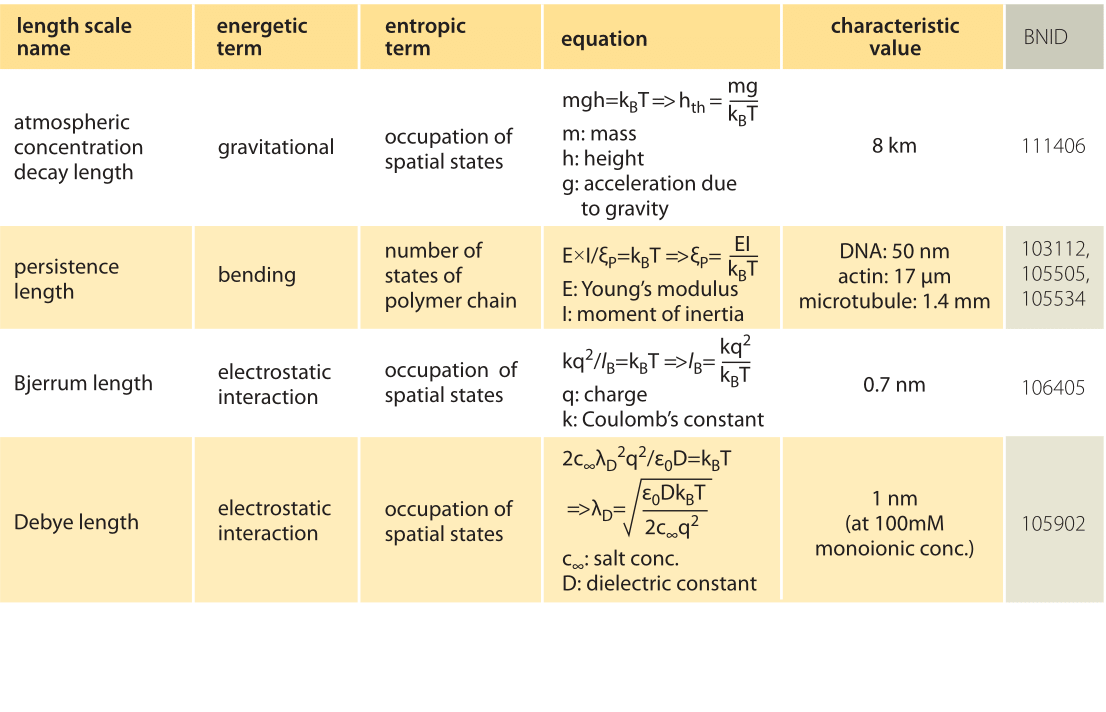
What is the thermal energy scale and how is it relevant to biology?
Molecules are engaged in incessant random motions as a result of their collisions with the molecules of the surrounding medium as described in our discussion of Brownian motion in the vignette “What are the time scales for diffusion in cells?“. What was not clear when Brown made the discovery of the motions that now bear his name is that his observations struck right to the heart of one of the most important organizing principles in all of biology, namely, the way in which the rich interplay between deterministic and stochastic energies dictates phenomena in nearly all the molecular processes of life.
The physical consequences arising from thermal forces are familiar to us all. For example, think of the drop off in the density of air as a function of altitude. The height dependence of the density of air reflects an interplay between the force of gravity, which implies an increasing potential energy investment as the molecules rise higher in the atmosphere, and the entropy benefit which comes from allowing the molecules to explore a larger volume by increasing their altitude
The simplest way to analyze the effects of the competition between energetic and entropic contributions to free energy in the setting of molecular and cell biology is to equate the deterministic energy of interest to kBT, which reflects the thermal energy scale. To see this play out in the familiar everyday example of the density as a function of the altitude, this strategy corresponds to equating the potential energy of the molecule, given by mgh, to the thermal energy kBT as noted in Table 1. Following this idea and solving for h we estimate a length scale of h=kBT/mg ≈ 10 km, which is indeed a good estimate for the height at which the density of the atmosphere is reduced significantly from its density at the surface of the Earth (more precisely, by a factor of e, the natural logarithm, i.e. ≈3 fold). In statistical mechanics, the balance struck between energy and thermal fluctuations is codified through the so-called Boltzmann distribution that tells us that the probability of a state with energy E is proportional to exp(-E/kBT), illustrating explicitly how the thermal energy governs the accessibility of microscopic states of different energy.
In the cellular context there are several important length scales which emerge as a result of the interplay between thermal and deterministic energies (for examples, see Table 1). If we think of DNA (or a cytoskeletal filament) as an elastic rod, then when we equate the bending energy and the thermal energy, we find the scale at which spontaneous bending can be expected as a result of thermal fluctuations, also known as the persistence length. For DNA this length has been measured at roughly 50 nm (BNID 103112) and for the much stiffer actin filaments it is found to be 15 μm (BNID 105505). The interplay between Coulomb interactions and thermal effects for the case of charges in solution is governed by another such scale called the Bjerrum length. It emerges as the length scale for which the potential energy of electrical attraction is equated to kBT and represents the distance over which electrostatic effects are able to dominate over thermal motions. For two opposite charges in water, the Bjerrum length is roughly 0.7 nm (BNID 106405).
The examples given above prepare us to think about the ubiquitous phenomena of binding reactions in biology. When thinking about equilibrium between a bound state and an unbound state, as in the binding of oxygen to hemoglobin, a ligand to a receptor or an acid HA and its conjugated base A-, there is an interplay between energies of binding (enthalpic terms) and the multiplicity of states associated with the unbound state (an entropic term). This balancing act is formally explored by thinking about the free energy DG. Thermodynamic potentials such as the Gibbs free energy take into account the conflicting influences of enthalpy and entropy. Though often the free energy is the most convenient calculational tool, conceptually, it is important to remember that the thermodynamics of the situation is best discussed with reference to the entropy of the system of interest and the surrounding “reservoir”. Reactions occur when they tend to increase the overall entropy of the world. The enthalpic term, which measures how much energy is released upon binding, is a convenient shorthand for how much entropy will be created outside of the boundaries of the system as a result of the heat release from that reaction.

Figure 1: Back of the envelope calculation showing how the pKa, related to concentrations can be derived from the electrostatic interactions thus connecting entropy and enthalpy. The case of an ionizable group where a positive charge (proton) can be released to media and thus has an associated pKa is analyzed. Two distances between the positive charge and a balancing negative charge in the protein are compared. The 0.15 nm decrease in distance translates to an increase of one unit of the pKa.
In light of these ideas about the free energy, we can consider how binding problems can be thought of as an interplay between enthalpy and entropy. The entropy that is gained by having an unbound particle is in the common limit of dilute solutions proportional to -ln(c/1M), where c is the concentration. We are careful not to enrage the laws of mathematics that do not allow taking a logarithm of a value that has units and thus divide by a standard concentration. The lower the concentration c, the higher the gain in entropy from adding a particle (note the minus sign in front of the logarithm). But how does one relate the entropy gained and the enthalpy? This linkage is made once again through the quantity kBT. Note that kBT ln([c]/1M) has units of energy, and stands for the entropic contribution to the free energy gained upon liberating the molecule of interest from its bound configuration. This will be compared to the energy released in the binding process. Whichever term is bigger will govern the direction the process will proceed, towards binding or unbinding. When the two terms are equal we reach a state of equilibrium with equal propensity for both bound and unbound states. By computing the condition for equality to hold we can determine the critical concentration at which the entropic and enthalpic terms exactly balance.
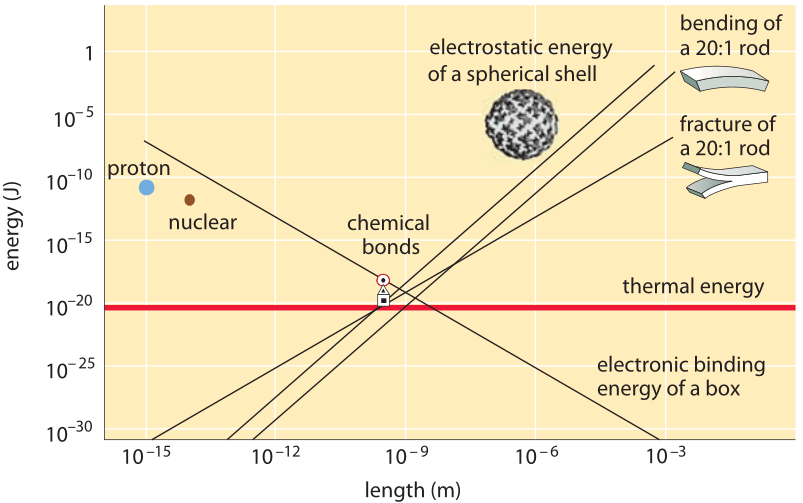
Figure 2: The convergence of the energies associated with many physical phenomena to a similar range at the nanometer length scale. Adapted from R. Phillips & S. Quake, Physics Today, 38, 2006.
Guided by this perspective, we now explore one of the classic case studies for every student of biochemistry. In particular, we examine how the pKa’s of amino acids can be understood as a competition. As shown in Figure 1, this competition can be understood as a balance between the entropic advantage of freeing up charges to let them wander around in solution and the energetic advantages dictated by interactions such as Coulomb’s law which tends to keep opposite charges in close proximity. The pKa is defined as the pH where an ionizable group (releasing H+) is exactly half ionized and half neutral. So the place of c in the equation for the entropy is taken by 10-[pKa] M. Armed with the understanding of this connection between pKa and the entropic term we can better appreciate the significance of pKa as a tuning parameter. Note from above that the entropy change upon liberating a molecule (or ion) at concentration c is ΔS=- kB ln(c/1M). For c=10-[pKa], this means the entropy change is given by ΔS=- pKa x kB ln(10). In particular, if the pKa is higher by one unit, the entropic term required to balance the energy of interaction (the enthalpic gain) is higher by a value of kBT·ln(10) (expressing kBT·ln(10) in units of kJ/mol we get 6 kJ/mol, the same value mentioned in the rule of thumb connecting concentration ratios and energies). If the interaction is a purely electrostatic one, we can interpret it using Coulomb’s law. The energy of two opposite charges in water increases by about kBT·ln(10) when the distance between the charges changes from 0.3 nm to 0.15 nm (both being characteristic interatomic distances). We thus note that if the charges are 0.15 nm closer (the difference of 0.3 and 0.15 nm), then the pKa will be one unit higher. This shows how in equilibrium, the stronger attractive interaction coming from the closer distance between the charges will lead to half ionization at a lower concentration of the separated charges in the solvent. Lower concentration means there is a higher associated entropic gain per separated charge and this higher gain is required to balance the attractive force. This is a manifestation, though quite abstract, we admit, of how forces and energies relate to concentrations.
It is interesting to observe how many physical processes have energies that are similar at the nanometer length scale as depicted in Figure 2. This makes the life of biomolecules intriguing as rather than having one major process dominating their interactions such as, say, gravitation for astronomical length scales, they are governed by an intricate interplay between, for example, electrostatic repulsion and attraction forces, mechanical deformations, thermal energy and chemical bonds energies.