How many chromosome replications occur per generation?

A look in the mirror tells us that we are made of many different types of cells. In terms of genetics and evolution, the most important distinction is between the cells of the germ line, those cells that have the potential to culminate in new offspring, and somatic cells, those cells that build the rest of the body but do not propagate to the next generation. This dichotomy is more relaxed in plants but in principle is similar. An important factor contributing to the fidelity with which the genetic information is transferred from one generation to the next is the number of cell divisions each germ cell will make on average before the actual fertilization event.

In a previous vignette on “How many cells are there in an organism?” we made the estimate that a human is made up of 3×10¹³ cells (BNID 109716). But cells are constantly born and dying. Given this turnover, how many cells does a person make in a lifetime? Though the question touches our very own composition, we could only find one passing mention of about 10¹⁶ cell divisions in total during a human lifespan (BNID 100379). Our sanity check on this value relies on knowing that red blood cells are the dominant cell type by sheer number in the body (bacteria aside) and that their lifetime is on the order of 100 days. So in 100 years of life there will be about 300 cycles of replacement for these red blood cells, and the inferred total number of cell divisions is indeed of order 10¹⁶ (≈2×10¹³ rbc cells/person x 300 cycles in lifetime). We proceed to analyze two very naïve and extreme models regarding how many replications of the chromosomes are required to obtain the somatic cells that lead to the next generation. In the first simplified model we assume, as depicted in Figure 1, that all cells divide in a symmetric manner like a binary bifurcating tree. The number of cells progresses in a geometrical series starting from 1 at the first generation to 2, 4, 8, 16 etc. We will thus have 2n cells after n replication rounds. 10¹³ cells will be reached after log2(10¹³) ≈ 40 replication rounds and 10¹⁶ cells after ≈50 replication rounds.

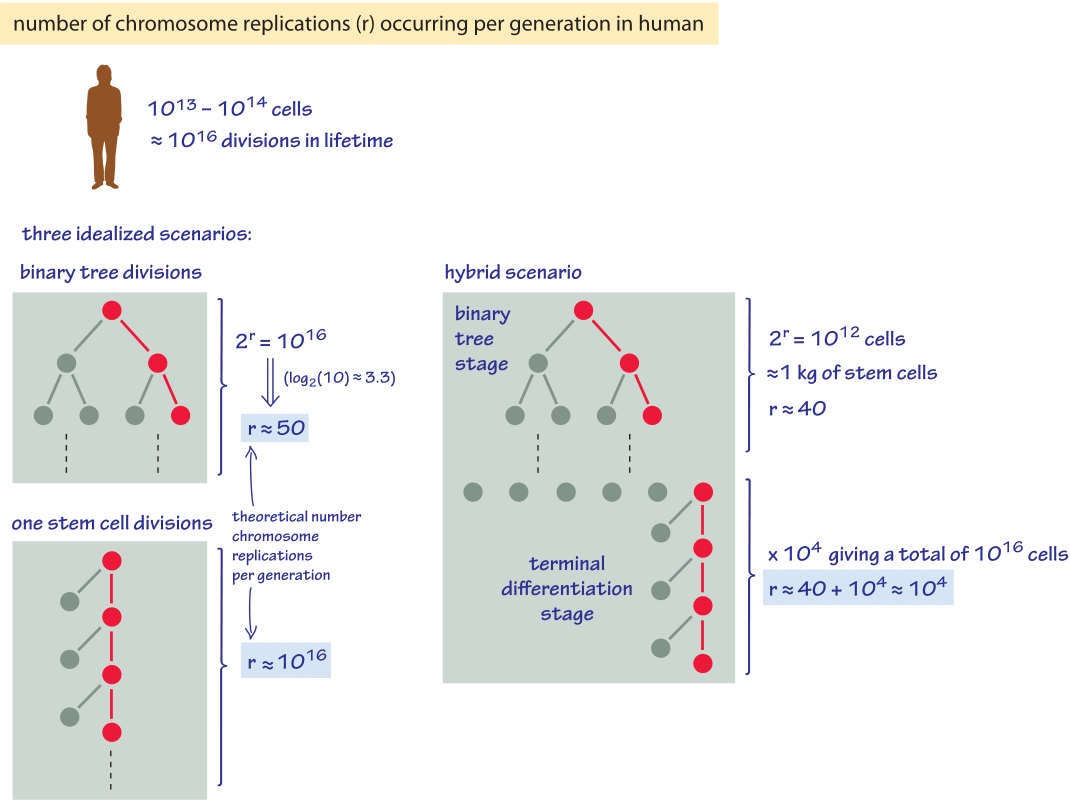
Figure 1: Back of the envelope calculation on how many chromosome replications occur per generation in two extreme scenarios. For the human case the average number of divisions a cell goes through in a lifetime is different by the astronomical ratio of 50 to 10¹⁶.

In our second toy model, we imagine an idealized process, schematically drawn in Figure 1, in which every cell in the body is a direct descendant of some single “stem cell”. In this case, the generation of the above mentioned full complement of a lifetime of cells in the human body would require 10¹⁶ replication rounds (maybe minus 1 to be accurate…) for the lifetime repository of cells.. Such a cell lineage model would place enormous demands on the fidelity of the replication process because mutations would accumulate as discussed in the vignette on “What is the mutation rate during genome replication?”.

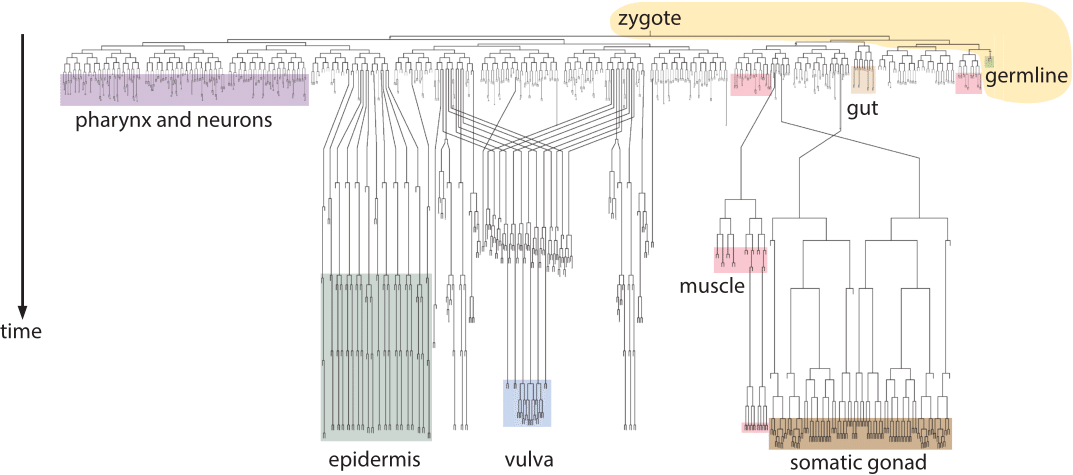
The cell lineage from egg to adult is closer to the tree of binary divisions described in the first model. Nowhere has this been illustrated more dramatically than in the stunning experiments carried out to map the fates and histories of every cell in the nematode C. elegans. In a Herculean effort in the 1970s Sir John Sulston and coworkers delineated the full tree for C. elegans, redrawn in Figure 2, by careful microscope observations of the development of this transparent nematode. We can see that for this remarkable organism with its extremely conserved developmental strategy, the depth of this tree from egg to egg is ≈9 replications (BNID 105572).

Figure 2: C. elegans lineage tree as deciphered through light microscopy

In larger multicellular organisms, the picture is very complex and can be thought of as a hybrid between the two simplified models as also noted in Figure 1, starting from a binary tree expansion stage that then turns into a terminal differentiation stage. Such complex structured models were observed in the crypts of the colon and in the apical meristem of plants. In plants for example, a small set of stem cells, say about 10 in a plant apical meristem, divide slowly in what is termed the quiescent center. These stem cells lead to a larger population of say 100 cells that divide rapidly to give the majority of cells. The rapidly dividing cells, which accumulate mutations, are slowly replaced before they accumulate too many mutations by the progeny of the slowly dividing stem cells.

Table 1: Number of chromosome replications leading to male sperm and to female ovule in different organisms

Estimates of the average number of replication rounds leading to adult cells in a range of organisms are given in Table 1. Normal mammalian cells that are not stem cells or cancerous cell lines usually stop dividing after about 40-60 cell cycles (BNID 105586). In humans, eggs are produced much earlier and in more restricted numbers than sperm cells. Indeed, there are much fewer chromosome replications from egg to egg (23, BNID 105585) versus sperm to sperm (from 35 at age 15, to >800 at age 50, BNID 105574). As mutations accumulate with replication rounds, most of the mutations arise in the male lineage. Indeed the ratio of mutations passed on by older fathers compared to mothers is about 4 to 1 (BNID 110290). Mothers are reported to pass about 15 mutations on average irrespective of age (BNID 110295) while 20 year-old fathers transmit about 25 mutations and 40 year-old fathers transmit about 65 mutations (BNID 110294). That is about 2 extra mutations per extra year of age of the father (BNID 110291). Some have gone so far as to suggest that the fact that older fathers are chiefly responsible for introducing mutations into the population, can provide a potential explanation for hemophilia in the British royal family whose kings kept on having children at advanced ages.

Should the number of divisions have implications for the occurrence of cancer, which has mutations and replication at its essence? Different types of cancers are known to have very different lifetime risks that span several orders of magnitude. Recently, the number of stem cells and their division rates are becoming available. In a recent study (C. Tomasetti & B. Vogelstein, Nature, 347:78, 2015), researchers collected the number of total stem cell divisions in a lifetime for 31 tissue types and correlated it to the lifetime risk of cancer occurring in that tissue. The correlation was found to be striking at about 0.8. This high correlation leaves only a much smaller fraction to be explained by environmental factors or genetic predispositions, though these have been at the center of research for decades. In our perspective this is a striking example of how paying careful attention to the numbers can still today bring simple insights into view.