How much energy is carried by photons used in photosynthesis?

Nuclear reactions taking place 150 million kilometers away in the sun’s interior are used to drive the bustling activity of life observed on planet Earth. The energy that drives these biological reactions is heralded by the arrival of packets of light from space known as photons. In this vignette, we interest ourselves in how much energy is carried by these photons.

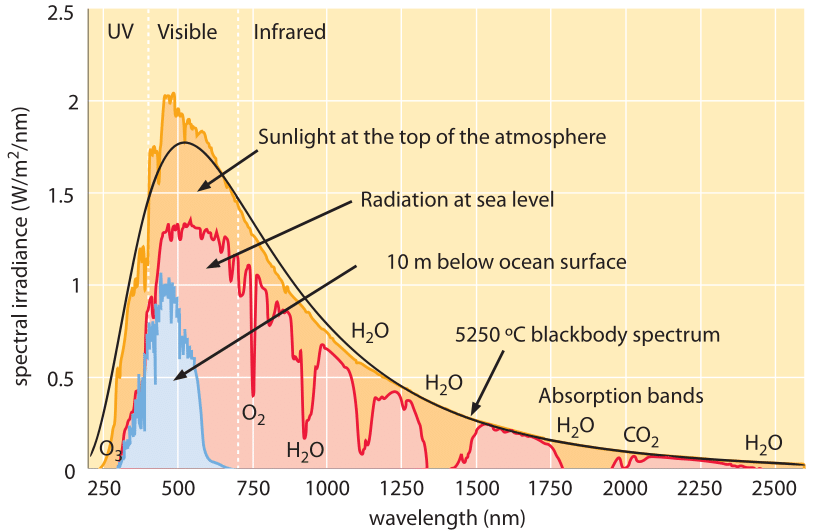
Figure 1: Spectrum of solar irradiation. The different curves show the radiation due to a blackbody at a temperature of ≈5500oC, the radiation density at the top of the Earth’s atmosphere and the radiation density at sea level. The various absorption peaks due to the presence of the atmosphere are labeled with the relevant molecular species. (Adapted from the National Renewable Energy Laboratory.)

Even though the nuclear reactions deep within the sun are taking place at temperatures in excess of a million degrees Kelvin, during the journey of a photon from the sun’s interior to its surface it is absorbed and reemitted numerous times and is only emitted for the last time near the sun’s surface where the temperature is much lower. The Sun’s emission spectrum is thus that of a blackbody at ≈5500^oC (Figure 1 and BNID 110208, 110209). However, as a result of our own atmosphere, the photons reaching the earth’s surface do not reflect a perfect blackbody spectrum since several wavelength bands get absorbed as shown in Figure 1, resulting in a spectrum full of peaks and troughs.

The overall process taking place in photosynthesis and serving as the energetic basis for our biosphere is depicted in Figure 2. To drive photosynthesis, a photon must be energetic enough to excite photosynthetic pigments. In particular, this excitation refers to the fact that an electron in the pigment needs to get shifted from one molecular energy level to another. These pigments are coupled in turn to the photochemical machinery that converts electromagnetic energy into chemical energy by producing charge separation. This charge separation takes several forms. One contribution comes from an imbalance of protons across membranes which drive the ATP synthases, the molecular machines that synthesize ATP, resulting in an end product of ATP itself. The second form of charge separation manifests itself in the form of reducing power, the term for transient storage of electrons in carriers such as NADP used later for stable energy storage in the form of sugars produced in the Calvin-Benson cycle. The redox reactions that drive the production of this reducing power are themselves driven by the light-induced excitation of pigments.

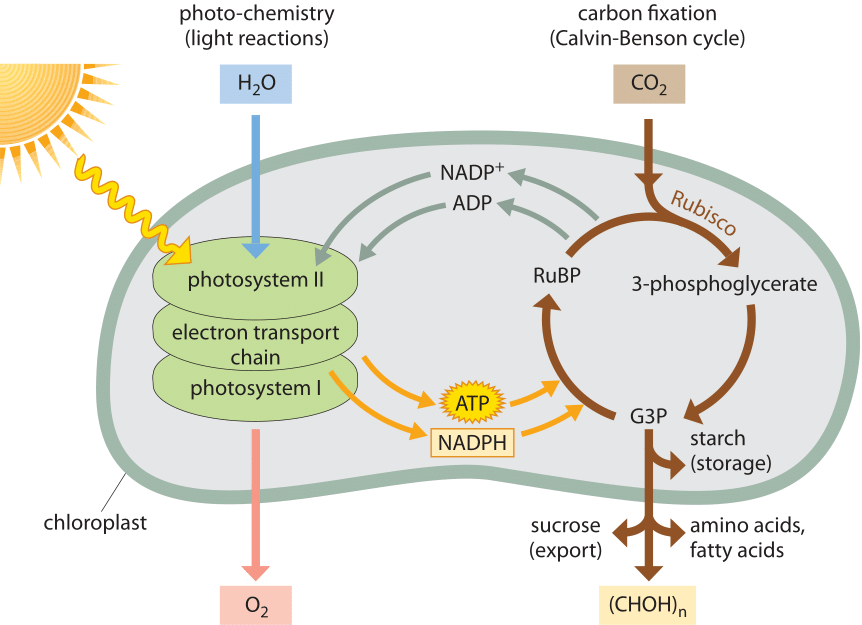
Figure 2: The flow of energy in the biosphere. Energy coming as photons from the sun is stored through photochemical reactions in ATP and NADPH while producing oxygen from water. These energy currencies are then used in order to fix inorganic carbon by taking carbon dioxide from the air and transforming it into sugars that are the basis for biomass accumulation and long-term energy storage in the biosphere.

The vast majority (>99.9%, J. A. Raven, Functional Plant Biology, 36:505, 2009) of these photochemical transformations are performed by the most familiar and important pigment of them all, namely, chlorophyll. In the chlorophyll molecule an electron moves to an excited energy level as a result of the absorption of a photon with wavelength ≤700nm. To convert wavelength into energy we exploit the famed Planck relation, E=hν, which relates the photon energy E, to its frequency ν via Planck’s constant, h. We then use the fact that the frequency times the wavelength λ is equal to the speed of light νλ=c. If we work using nm units to characterize wavelengths, this relation can be rewritten as E=hc/λ ≈1240/λ, where energy is expressed in eV (electron volts). We thus get an energy scale of 1.8 eV at 700 nm. This unit of energy is equivalent to the energy that an electron will gain when moving across a potential difference of 1.8 volts. To transform into more familiar territory, it is equivalent to ≈180 kJ/(mol photons) or ≈70 k_BT/photon. This is equivalent, in turn, to several times the energy associated with the hydrolysis of ATP, or the transfer of protons across the cell’s membrane and is thus quite substantial at the molecular scale.

Using Figure 1 we can estimate the overall energy flux associated with the incident photons and how many such photons there are. A crude but simple approximation is to replace the actual spectrum by a rectangle of width ≈1000 nm (between 300 nm and 1300 nm) and height ≈1 W/m²/nm. Based on these values the area under the curve is roughly 1000 W/m² which is quite close to the measured value for the mean incident power per unit area measured at the Earth’s surface. As an aside, 1 kW is the average electrical power consumption per person in the western world.

How many photons make up this steady stream of incident radiation? If we make yet another simplifying assumption, namely, that all photons have the same energy as that we calculated above for a 700 nm photon, 180 kJ/(mole photons) we estimate that there are ≈1000 [W/m²]/180[kJ/mol] ≈ 5 mmol photons/s·m². The unit corresponding to 1 mole of photons per square meter bears the name of Albert Einstein, and our estimates show us that the number of photons incident on a 1 m² area each second is ≈5000 microEinsteins, or about 3×10²¹ photons. More than half of these photons are actually invisible to us, located in the infrared wavelength range (above 700 nm). Photons are absorbed by pigments such as chlorophylls that have effective cross sections for absorption of about 10^-21 m² (BNID 100339). Given the photon flux on the order of 10²¹ photons/m² we infer about one excitation per chlorophyll per second.

The process of photosynthesis is the main reason for humanity’s usage of land and fresh water resources through the practice of agriculture. The efficiency of this conversion of light energy into mostly grains is performed at an efficiency that in well-cultivated conditions reaches about 1% (BNID 100761). Though it sounds low, one should appreciate the number of hurdles faced along the way. About half the incident energy occurs at infrared wavelengths and does not excite the chlorophyll molecules that convert the photons to excited electrons. Short wavelengths excite the chlorophyll but the energy beyond the minimal excitation energy is quickly dissipated causing on the average roughly another loss of a factor of 2. The light and dark reactions usually get saturated at about a tenth of the maximal sun intensity and a process of photoinhibition diverts that energy into heat. Of the energy harvested and stored as sugar about half is used by the plant to support itself through respiration. Finally the harvest index, which is the fraction of biomass that can be consumed, is rarely more than one half. A crude rule of thumb is that a square meter will produce about 1 kg per year of edible dry mass.

People working on photosynthesis are often asked: “Can you make a human that relies on photosynthesis and does not have to eat?”. The short answer is no and that is where the discussion usually ends. But let’s entertain the possibility of covering the skin with photosynthetic tissue. The human skin is about 1 m² in area (BNID 100578). At a characteristic efficiency of 1% this will yield under the peak 1000 W/m² noon sun about 10 W, which is still an order of magnitude lower than human requirements as discussed in the vignette on “What is the power consumption of a cell?”.