What is the energy scale associated with the hydrophobic effect?
Water is a polar material. This means that water molecules have a charge distribution that results in a net dipole moment. As a result of this important feature, when foreign molecules that do not themselves have such a dipole moment (such as hydrophobic amino acids, for example) are placed in water, the resulting perturbation to the surrounding water molecules incurs a free energy cost. Interestingly, from a biological perspective, this free energy cost is one of the most important driving forces for wide classes of molecular interactions, many of which lead to the formation of some of the most famed macromolecular assemblies such as lipid bilayers and viruses.
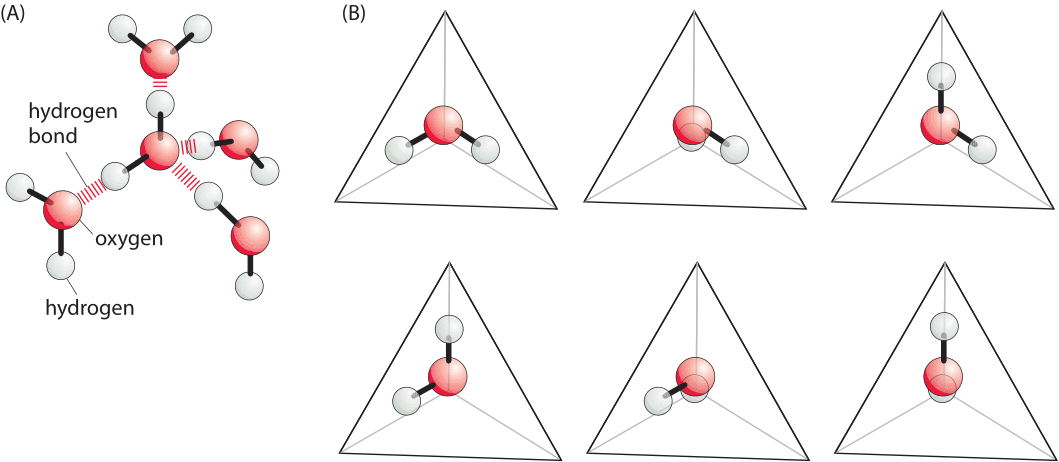
Figure 1: Simplified model of the hydrophobic effect. (A) A simplified model for possible orientations of water molecules in a tetrahedral network. (B) Each image shows a different arrangement of the water molecule that permits the formation of hydrogen bonds with neighboring water molecules. The hydrogen bonds are in the directions of the vertices that are not occupied by hydrogens in the figure. Formation of a hydrophobic interface deprives the system of the ability to explore all of these different states thus reducing the entropy. Adapted from Ken Dill, molecular driving forces.
This energetic effect, most commonly observed in water, is termed the hydrophobic effect. Though the hydrophobic effect is extremely subtle and depends upon the size of the solute, for large enough molecules the hydrophobic effect can be approximated as being proportional to the area of the interface (so called interfacial energy). Specifically, for sufficiently large solutes in water, the energy penalty arising from adding a non-polar area within water, can be approximated as an interfacial energy of ≈4kBT/nm2 or ≈10kJ/mol/nm2 (BNID 101826). There is a long and rich theoretical tradition associated with trying to uncover the origins of this free energy penalty and for our discussion we adopt a particularly simple heuristic perspective, cognizant of the fact that a full theoretical treatment is fraught with difficulties. The argument goes that when a molecule with a “hydrophobic interface” is placed in water, the number of conformations (shown in Figure 1) of the surrounding water molecules is decreased. Since these water molecules have fewer accessible states, they have lower entropy and hence the situation is less favorable in terms of free energy. Using this simple model suffices to estimate the free energy scale associated with hydrophobic interactions that was presented above, though it breaks down for small solutes where the hydrogen binding network can readjust itself around the solute. In relation to the simplified conformations shown in Figure 1, it is suggested that next to the interface only say 3 of the 6 will be possible as the others will not have a way to make hydrogen bonds. This illustrates how the conformation of the tetrahedral network of hydrogen bonds is thought to be compromised when a nonpolar molecule is placed in solution. If there are 10 water molecules per nm2 of interface (each ≈0.3nm in size), and the number of conformations for each molecule decreased by a factor of 2, the free energy cost is 10xkBTxln(2)/nm2 which is within a factor of 2 of the measured value.
To get a better feeling for these numbers, consider an O2 molecule dissolved in water. We can estimate the area of contact with the surrounding water by thinking of a box ≈0.2 nm on each side. This gives an area of ≈6*0.22 ≈ 0.2 nm2, resulting in a free energy penalty of about 1 kBT. Every kBT translates to an equilibrium concentration in water that is lower by a factor of e (2.718…), based on the Boltzmann distribution which states that a difference of energy E translates into a decreased occupancy of e-E/kBT. Non-polar metabolites which are an order of magnitude larger in area will have a prohibitively large free energy cost and are thus not soluble in water. A parallel challenge exists with polar compounds such as peptides, RNA, and metabolites that have small occupancy in hydrophobic environments and are thus restrained from transferring across the non-polar, hydrophobic lipid -bilayer membranes of cells.
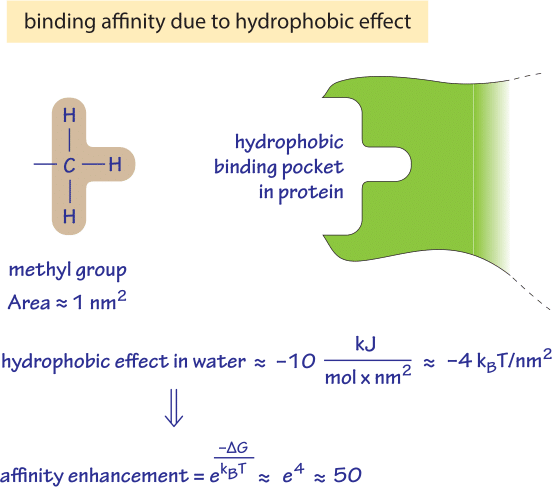
Figure 2: Back of the envelope calculation of what increase in binding affinity one could expect from the hydrophobic effect resulting from a single methyl group buried in a hydrophobic binding pocket.
The hydrophobic effect can play a significant role in determining the affinity of binding of a metabolite to an enzyme as shown schematically in Figure 2. A methyl group has a surface area of about 1 nm2. A non-polar surface initially exposed to water that gets buried within a hydrophobic binding pocket has a predicted stabilizing free energy gain of ≈10kJ/mol/nm2. For a methyl group we thus find a free energy difference of ≈10kJ/mol≈4kT which translates into an affinity enhancement of ≈e4 ≈ 50 fold as derived in the calculation in Figure 2.
These same types of arguments can be made for many of the most important macromolecules in the cell ranging from the contributions to the driving force for protein folding to the basis of protein-protein contacts such as those between the repeated subunits that make up a viral capsid to the ways in which lipids congregate to form lipid bilayers. The lipid effect is best illustrated through the way in which the critical micelle concentration (i.e. that concentration at which free lipids will no longer be tolerated in solution and they come together to make little spheres) depends upon both the lengths and number of tails in the lipid molecule. In this case, the hydrophobic cost for a given lipid scales linearly as n, the number of carbons in its tail. The corresponding critical micelle concentration depends exponentially on this value of n as observed experimentally.

