Wheels are a remarkable human invention that revolutionized our mobility. Interestingly, rotary motion is not exclusively the province of humans, though it has sometimes been argued that human ingenuity outpaced nature on the grounds that “nature did not invent the wheel”. Different rationalizations for the putative absence of wheels have been put forward to explain this apparently surprising observation, ranging from developmental and anatomical constraints to the absence of a selective advantage for such wheels. However, in fact, cells of all kinds exploit rotary motion, whether in the form of the ATP-synthase machines that generate ATP or the motors that power flagella to propel cells forward.

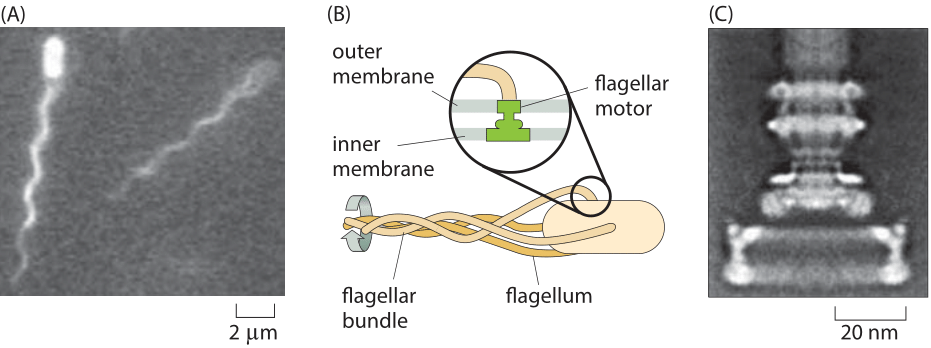
Figure 1: Flagellar-based motility in E. coli. (A) Two E. coli cells and their bundle of fluorescently labeled flagella. (B) Schematic of the bundling of flagella that drives bacterial motility. The inset shows how the rotary motor is embedded in the cell membrane. (C) Electron microscopy image of the rotary motor. (C adapted from H. C. Berg, Phys. Today, 53:24, 2000.)

Perhaps the most well known example of molecular rotary motion is that of the flagella that drive the swimming behavior of E. coli and other bacteria. This model system is also a foundational example of cell signaling, where dissection of the signal transduction in chemotaxis has made it possible to give a quantitative explanation of “behavior” in molecular terms. The motion of these bacteria is driven by the rotation of one to ten flagella (Figure 1A, BNID 100100) that are propelled by an exquisite rotary motor (Figure 1B).  The free energy that drives these motors is provided by protons moving down a transmembrane electrochemical potential gradient. The flagellar motor rotates at 100 turns per second under normal motility speed and can reach a maximal speed of around 300 turns per second (BNID 103813, 109337), a rate that surpasses the rapid turbine blades of modern jet engines.

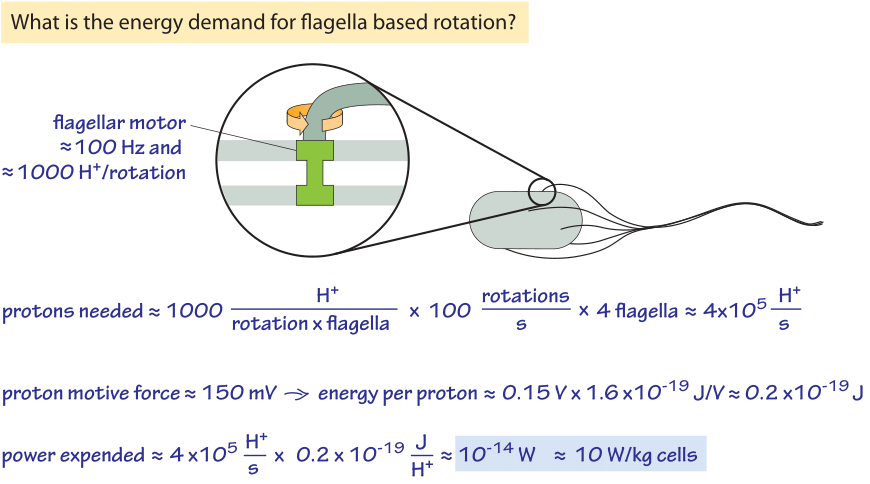
Figure 2: Back of the envelope calculation showing the energy requirements for bacterial motility. For slow growing or stationary phase bacteria the power expended can be a non-negligible fraction of their overall energy budget.

The rotation of the flagellar motor is energized by the cell’s membrane serving as a circuit element known as a capacitor. Pumps that continuously pump protons out of the cell ensure that this energy source is not drained by maintaining an imbalance in the electrochemical potential across the membrane. One interesting question raised by this process is how much power does motility require and how efficient is the motor? Figure 2 provides a schematic of the conceptual framework we use to make an estimate of the efficiency of these motors. About 1200 protons were measured to flow through the motor per revolution (BNID 109759). This number is roughly consistent with our knowledge that each motor is composed of about 11 stator complexes (with four copies of MotA protein and two copies of MotB protein each, BNID 109768) and was measured to take 26 steps per rotation (BNID 110614). Each complex at each step requires about 2-4 protons. So with ≈1200 H⁺/rotation, and say 4 flagella rotating at ≈100 Hz we get a proton consumption rate of 5×10⁵ H⁺/s. Each proton transfer releases about 0.15 eV or 0.2×10^-19 J (see vignette on the trans-membrane potential) and so 5×10⁵ H+/s release about 10^-14 W. The power required for driving a sphere the size of an E. coli at a velocity of ≈30 μm/s (BNID 109419) against the force of viscosity can be calculated based on the Einstein-Stokes equation as elegantly derived in the classic book on random walks in biology by Howard Berg. This theoretical value for the minimal needs for motility is 10^-17 W and so we find that the “efficiency” is about 10^-17/10^-14=0.1%. Edward Purcell showed that with a helical flagellum one cannot have an efficiency higher than 1%. So this mode of motility is not very energy efficient, but it works all the same, which is not an easy feat as can be appreciated by reading one of the alltime favorite papers of physicists on biology, namely,  “Life at low Reynolds number”. Should bacteria care about the efficiency of the process of cellular motility? Consulting the vignette on the power consumption of a bacteria we remind ourselves that at fast growth rates a bacterium uses about 10^-12 W which makes the motility cost about 1% of the total energetic budget. When the cell is starved the maintenance energy is about 10^-14 W and so the motility energy requirements are expected to be a significant fraction of the total.

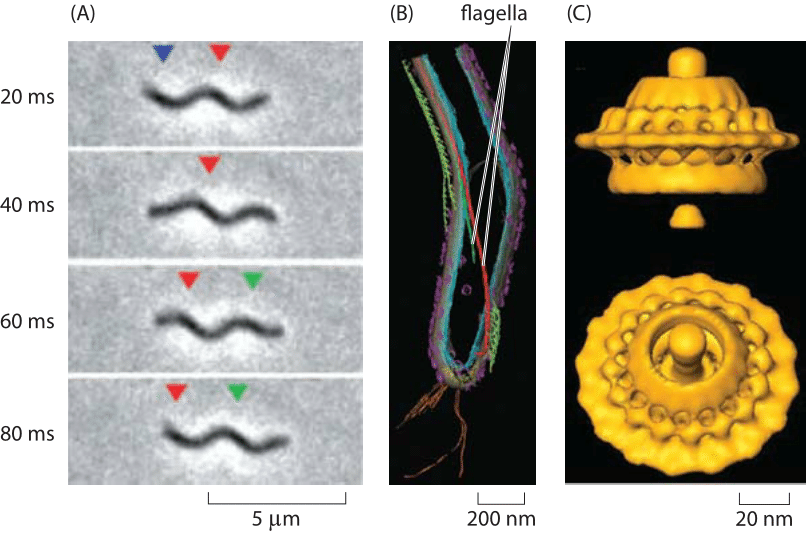
Figure 3: Spirochaete motility powered by periplasmic flagella. (A) A swimming T. primitia cell shown at various times during a swimming trajectory. (B) Cryo-electron microscopy image reconstruction of the internal flagella. (C) The molecular motor that powers rotation of the flagellum. (A, B adapted from G. E. Murphy et al., Molecular Microbiology, 67:1184, 2008; C adapted from G. E. Murphy et al., Nature, 442:1062, 2006.)

The diversity of life has become one of our typical refrains and rotary motion is no exception. Beyond the E. coli paradigm are all sorts of other interesting and bizarre examples of rotary motion. One such example is presented by the periplasmic flagella of the spirochaete Treponema pimitia which is characterized by the spinning of its flagellum within the cell, resulting in a corkscrew motion of the cell as shown in Figure 2. Like its E. coli counterpart, the rotary motor that controls this flagellum can turn as fast as 300 Hz (BNID 103813) and has a structure with many of the same key features of an exterior flagellum as depicted in Figure 3.

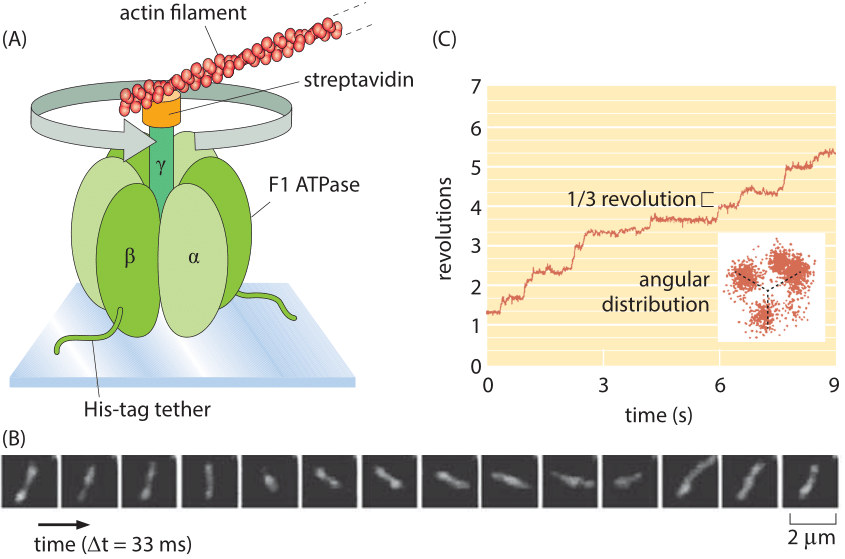
Figure 4: Single-molecule observation of a rotary motor using actin filaments to reveal the motor rotation. (A) The F1 portion of ATP synthase is tethered to a glass slide. The rotation of the complex is monitored by attaching a fluorescently labeled actin filament. (B) Fluorescence images of the F1 shaft as it turns. (C) At low ATP concentrations, the rotation occurs in three evenly spaced angular substeps. The graph shows the angular revolution for a single actin filament over a period of a few seconds and the inset shows the positions of the filament end over a longer movie. (A, B, adapted from H. Noji et al., Nature 386:299, 1997; C, adapted from R. Yasuda et al., Cell 93:1117, 1998.)

Rotary motion is a part of many cell’s “gadgets” in contexts beyond motility.  Indeed, some have ventured that the world’s second most important molecule is the ATP-synthase protein complex which is responsible for the enormous ATP biosynthetic flux central to organisms ranging from bacteria to humans. The study of the dynamics of this rotary motor culminated in one of the most beautiful of single-molecule experiments in which the rotation of individual synthases was followed in real time by attaching actin filaments to the top of the motor as shown in Figure 4.  In the in vivo setting, also these complexes rotate at ≈300 turns per second (at 37⁰C deg, BNID 104890)

Interestingly, the ATP synthase as well as many other processes use the same power source as the flagellar motor, namely, relying on the transmembrane voltage created by pumps. In times of need, when these pumps cannot function, the ATP synthase rotor can reverse direction in order to ensure the capacitor keeps its charge. It then breaks down ATP and moves protons up the chemical gradient thus replenishing the original driving force.  So this machine is actually a dual-purpose rotor.