What are the concentrations of different ions in cells?

Beginning biology students are introduced to the macromolecules of the cell (proteins, nucleic acids, lipids and carbohydrates) as being the key players in cellular function.  What is disturbingly deceptive about this picture is that it makes no reference to the many ion species without which cells could not function at all.   Ions have a huge variety of roles in cells.  Several of our favorites include the role of ions in electrical communication (Na⁺, K⁺, Ca²⁺), as cofactors in dictating protein function with entire classes of metalloproteins (constituting by some estimates at least ¼ of all proteins) in processes ranging from photosynthesis to human respiration (Mn²⁺, Mg²⁺, Fe²⁺), as a stimulus for signaling and muscle action (Ca²⁺), and as the basis for setting up transmembrane potentials that are then used to power key processes such as ATP synthesis (H⁺, Na⁺).

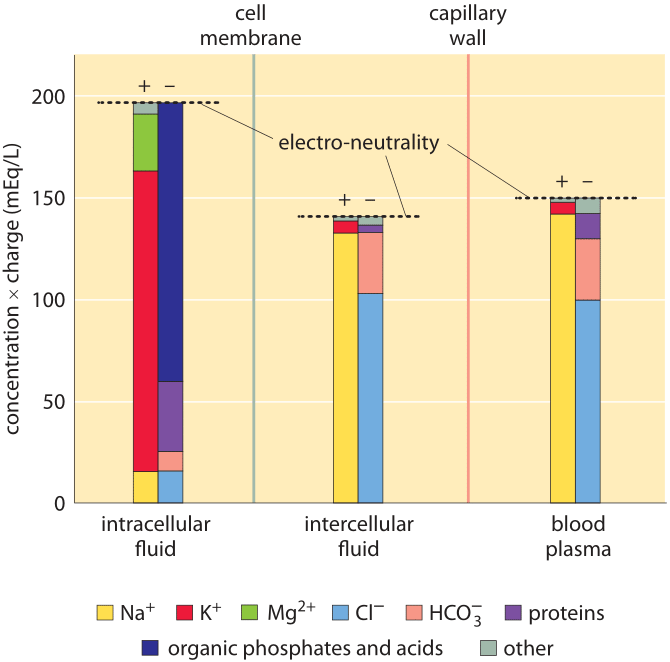
Figure 1: Ionic composition in mammalian organisms. Three distinct regions are characterized: the cellular interior (“intracellular fluid”), the medium between cells (“intercellular fluid”) and the blood plasma that is outside the tissue, beyond the capillary wall. The y-axis is in units of ionic concentration called Eq for “equivalents”, which are equal to the ion concentration multiplied by its absolute charge. These units make it easy to see that the total amount of positive and negative charge is equal in each compartment, in line with the principle of electro-neutrality. Even though it is not evident from the figure, the total free solute concentrations (sum of concentrations of both positive and negative components not taking into account their charge) are the same in the intracellular and intercellular fluid. This reflects that the two compartments are in osmotic balance. (Adapted from O. Andersen, “Cellular electrolyte metabolism” in Encyclopedia of Metalloproteins, Springer, pp. 580-587, 2013, BNID 110754.

A census of the ionic charges in a mammalian tissue cell as well as in the surrounding intercellular aqueous medium in the tissue is shown in Figure 1 left and middle panels. The figure also shows the composition of another bodily fluid, the blood plasma, which is separated from tissues through the capillary walls. The figure makes it clear that in each region the sum of negative ion charges equals the sum of positive charges to a very high accuracy. This is known as the law of electroneutrality. The relatively tiny deviations we might expect are quantified in the vignette on “What is the electric potential difference across biological membranes?”. Figure 1 also shows that blood ionic composition is very similar to that of the interstitial fluid. Yet, the composition of the cell interior is markedly different from the milieu outside the cell. For example, the dominant positive ion within the cell is potassium with a concentration that is more than 10-fold higher than that of sodium. Outside the cell the situation reverses with sodium as the dominant positive ion. These and the other differences are carefully controlled by both channels and pumps and we discuss some of their functional importance below.

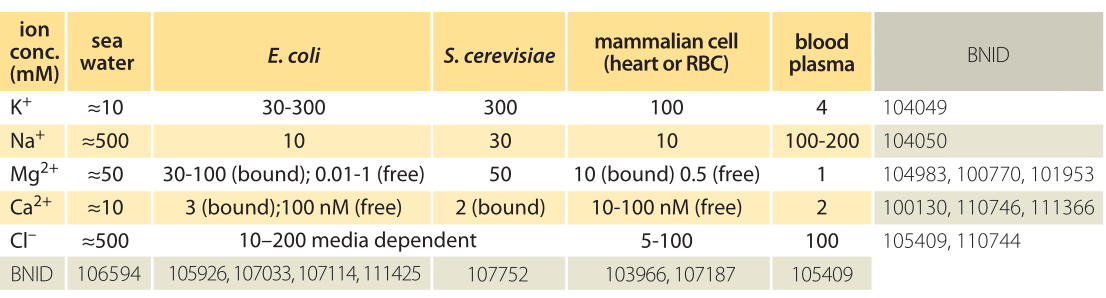
Table 1: Ionic concentrations in sea water, a bacterial and yeast cell, inside a mammalian cell and in the blood. Concentrations are all in units of mM. Values are rounded to one significant digit. Unless otherwise noted, concentration is total including both free and bound ions. Note that concentrations can change by more than an order of magnitude depending on cell type and physiological and environmental conditions such as the medium osmolarity or external pH. Na+ concentrations are especially hard to measure due to trapping and sticking of ions to cells. Most Mg2+ ions are bound to ATP and other cellular components. More BNIDs used to construct table: 104083, 107487, 110745, 110754.

Ion channels serve as passive barriers that can be opened or closed in response to environmental cues such as voltage across the membrane, the concentration of ligands or membrane tension.   Pumps, by way of contrast, use energy in the form of protons or ATP in order to pump charged species against their concentration gradient. The differences in concentration mediated by these membrane machines can often be several orders of magnitude and in the extreme case of calcium ions correspond to a 10,000-fold greater concentration of ions outside of the cell than inside as shown in Table 1. The dominant players in terms of abundance inside the cell are potassium (K⁺), chloride (Cl^–) and magnesium (Mg²⁺) (though the latter is mostly bound to ATP, ribosomes and other macromolecules and metabolites such that its free concentration is orders of magnitude lower). Table 1 shows some typical ionic concentrations in bacteria, yeast and mammalian cells. Some ion concentrations are regulated tightly, particularly toxic metal ions that are also essential for certain processes, but also regulation of K⁺ by osmolarity, which is essential for growth. Other ions are less tightly regulated, Na⁺ being one such example. One of the provocative observations that emerges from this table is that positive ions are much more abundant than negative ions. What is the origin of such an electric imbalance in the simple ions? Many of the metabolites and macromolecules of the cell are negatively charged. This negative charge is conferred by phosphate in small metabolites and DNA and by carboxylic groups on the acidic amino acids, such as the most abundant free metabolite, glutamate. Much more on these cellular players can be found in the vignette on “What are the concentrations of free metabolites in cells?”.

Potassium is usually close to equilibrium in animal and plant cells. Given that its concentration inside the cell is about 10 to 30 fold higher than outside the cell, how can it be in equilibrium? Assume we start with this concentration difference across the membrane, and with no electric potential difference (there are counter ions on each side of the membrane to balance the initial charges and they cannot move). As the potassium ions diffuse down their concentration gradient, from the inside to the outside, they quickly create an electric potential difference due to their positive net charge (the net charge movement is miniscule compared to the ion concentrations on the two sides of the membrane as discussed in the vignette on “What is the electric potential difference across membranes?”). The potential difference will increase until its effect will exactly balance the diffusive flux and this is when equilibrium will be reached. This type of equilibrium is known as electrochemical equilibrium. Indeed from the equilibrium distribution we can infer that the cell has a negative electric potential inside and by how much. The direction of the voltage difference across the cell membrane is indeed from positive outside to negative inside as can be naively expected from pumping of protons out of the cell, and as discussed in quantitative terms in the vignette on “What is the electric potential difference across membranes?”.

The concentrations described above are in no way static. They vary with the organism and the environmental and physiological conditions. To flesh out the significance of these numbers, we examine a case study from neuroscience.   For example, how different is the charge density in a neuron before and during the passage of an action potential? As noted above, the opening of ion channels is tantamount to a transient change in the permeability of the membrane to charged species. In the presence of this transiently altered permeability, ions rush across the membrane as described in detail in the vignette on “How many ions pass through an ion channel per second?”. But how big a dent does this rush of charge actually make to the overall concentrations? Muscle cells in which such depolarization leads to muscle contraction often have a diameter of about 50 μm, and a simple estimate (BNID 111449) reveals that the change in the internal charge within the cell as a result of membrane depolarization is only about a thousandth of a percent (10^-5) of the charge within the cell. This exemplifies how minor relative changes can still have major functional implications.